|
|
|
|
Blocky velocity inversion by hybrid norm |
The previous regularizations show that only a first derivative can create blockiness. However, using the first derivative means that we must pick a direction each time we apply the derivative. As a first test, we pick two directions: the vertical and horizontal as follows:
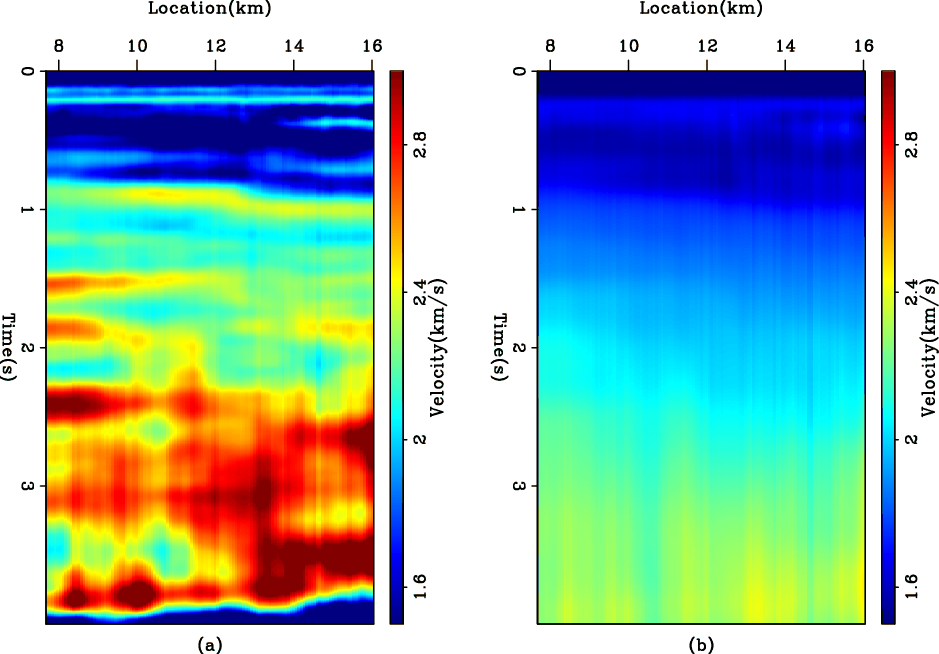
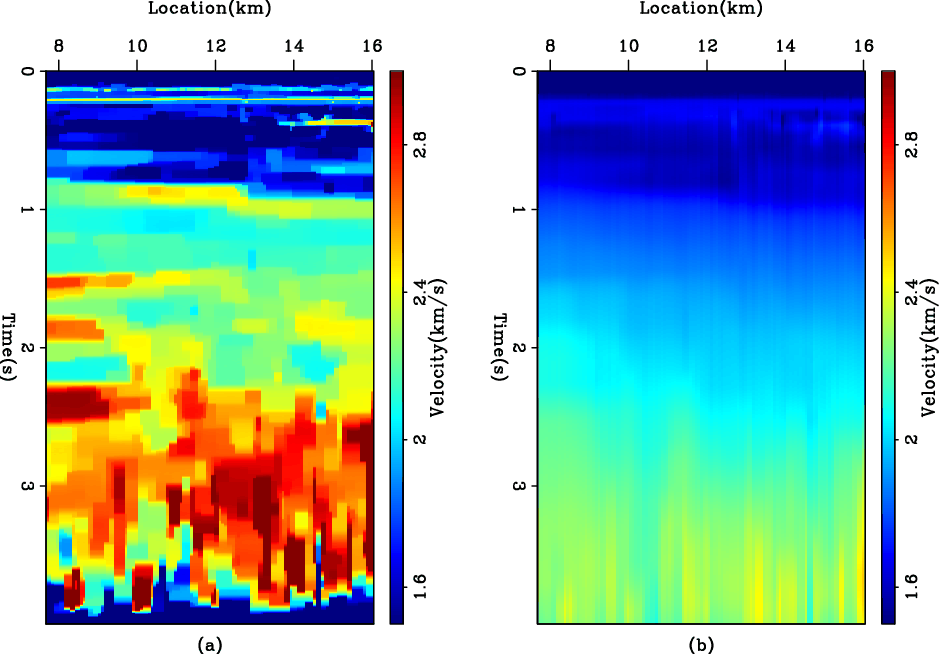
Figure 7 shows the results of using the ![]() norm with two first derivative applications, and Figure 8 shows the results of using the hybrid norm. Blockiness is clearly present in the hybrid norm results. However, there seems to be a preference for the sharp boundaries to be either horizontal or vertical, which is due to the directions of the derivatives we chose.
norm with two first derivative applications, and Figure 8 shows the results of using the hybrid norm. Blockiness is clearly present in the hybrid norm results. However, there seems to be a preference for the sharp boundaries to be either horizontal or vertical, which is due to the directions of the derivatives we chose.
|
|---|
|
l2-lab39
Figure 7. The WG dataset. (a) The interval velocity estimated by using the first derivative operator in two directions as a regularization in the |
|
|
|
|---|
|
hbe-lab37
Figure 8. The WG dataset. (a) The interval velocity estimated by using the first derivative operator in two directions as a regularization in the hybrid norm. (b) The reconstructed RMS velocity. |
|
|
|
|
|
|
Blocky velocity inversion by hybrid norm |