




Next: Constrained results
Up: Methodology
Previous: Methodology
In dealing with noise and certain geological features such as faults and angular unconformities, it is necessary to apply a weight to the flattening method. This weight is applied to the residual to ignore fitting equations that are affected by the bad dips estimated at faults. In the case of angular unconformities, it can be used to disable the vertical regularization in locations where multiple horizons converge.
The resulting weighted and constrained Gauss-Newton equations are now
iterate {
| 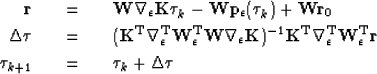 |
(17) |
| (18) |
| (19) |
} .
Again, I solve equation (18) efficiently using preconditioned conjugate gradients with equation (13) as the preconditioner and 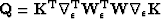 and
and 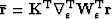 .
.





Next: Constrained results
Up: Methodology
Previous: Methodology
Stanford Exploration Project
1/16/2007
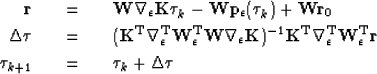
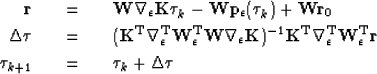
![]() and
and ![]() .
.