




Next: Constrained solution with weights
Up: Lomask: Improved flattening with
Previous: Introduction
Constraints were first applied to the flattening problem in Lomask and Guitton (2006).
In the 3D Gauss-Newton flattening approach, data is flattened by iterating over the following equations
iterate {
| 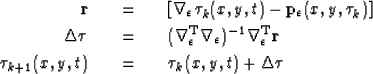 |
(1) |
| (2) |
| (3) |
} ,
where the subscript k denotes the iteration number,  is the estimated time-shift found in the least-squares sense so that its gradient matches the dip
is the estimated time-shift found in the least-squares sense so that its gradient matches the dip 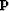 , and
, and  is an adjustable regularization controlling the amount of conformity in the time (or depth) dimension.
is an adjustable regularization controlling the amount of conformity in the time (or depth) dimension. 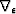 is a 3D gradient operator with an
is a 3D gradient operator with an  parameter.
The residual update in equation (1) can be rewritten as
parameter.
The residual update in equation (1) can be rewritten as
| ![\begin{displaymath}
\bf r \quad = \quad { \boldsymbol{\nabla}_\epsilon \boldsymb...
...}
{c}{{\bf b}} \\ {{\bf q}} \\ {\bf 0} \end{array} \right] }.\end{displaymath}](img6.gif) |
(4) |
I wish to add a model mask 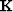 to prevent changes to specific areas of an initial
to prevent changes to specific areas of an initial 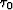 field. This initial
field. This initial 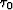 field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask I follow a similar development to Claerbout (1999) as
field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask I follow a similar development to Claerbout (1999) as
| 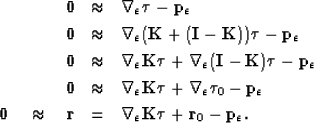 |
(5) |
| (6) |
| (7) |
| (8) |
| (9) |
The resulting equations are now
iterate {
| 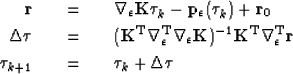 |
(10) |
| (11) |
| (12) |
} .
Because the mask 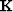 in equation (11) is non-stationary, I solve it using preconditioned conjugate gradients. The preconditioner efficiently exploits Discrete Cosine Transforms(DCTs) to invert a Laplacian operator Lomask and Fomel (2006) as:
in equation (11) is non-stationary, I solve it using preconditioned conjugate gradients. The preconditioner efficiently exploits Discrete Cosine Transforms(DCTs) to invert a Laplacian operator Lomask and Fomel (2006) as:
| ![\begin{displaymath}
\Delta \boldsymbol{\tau} \approx {\rm DCT_{3D}}^{-1} \left[{...
...abla_\epsilon\it{^{\rm T}}{\bf r} \right]}\ \over { J} \right],\end{displaymath}](img11.gif) |
(13) |
where 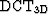 is the 3D discrete cosine transform and
is the 3D discrete cosine transform and
| 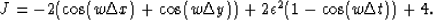 |
(14) |
J is the real component of the Z-transform of the 3D finite difference approximation to the Laplacian with adjustable regularization.
Following an approach for weighted 2D phase unwrapping by Ghiglia and Romero (1994), I define 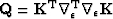 and
and 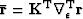 so that equation (11) becomes
so that equation (11) becomes
| 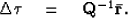 |
(15) |
For each non-linear Gauss-Newton iteration, the least-squares solution to equation (11) is solved by iterating over the following preconditioned conjugate gradients computation template:
iterate {
solve 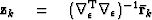 using equation (13)
subtract off reference trace
using equation (13)
subtract off reference trace 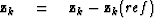 if first iteration {
if first iteration {
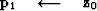 } else{
} else{
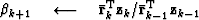
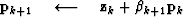 }
}
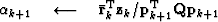
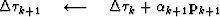
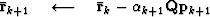 }
}
Here, k is the iteration number starting at k=0. It is necessary to subtract off the reference trace at each iteration because the Fourier based solution using equation (13) has no non-stationary information such as the location of the reference trace. Subtracting the reference trace removes a zero frequency shift. Nonetheless, in practice equation (13) makes an adequate preconditioner because 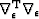 is often close to
is often close to 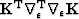 .
.
Convergence can be determined using the same criterion described in Lomask et al. (2006). Alternatively, an adequate stopping criterion would be to consider only the norm of the residual 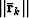 . This is essentially the average of the divergence of the remaining dips, i.e. ,
. This is essentially the average of the divergence of the remaining dips, i.e. ,
| 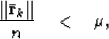 |
(16) |
where 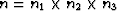 is the size of the data cube.
is the size of the data cube.
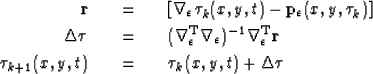
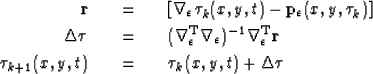
![\begin{displaymath}
\bf r \quad = \quad { \boldsymbol{\nabla}_\epsilon \boldsymb...
...}
{c}{{\bf b}} \\ {{\bf q}} \\ {\bf 0} \end{array} \right] }.\end{displaymath}](img6.gif)
![]() to prevent changes to specific areas of an initial
to prevent changes to specific areas of an initial ![]() field. This initial
field. This initial ![]() field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask I follow a similar development to Claerbout (1999) as
field can be picks from any source. In general, they may come from a manually picked horizon or group of horizons. These initial constraints do not have to be continuous surfaces but instead could be isolated picks, such as well-to-seismic ties.
To apply the mask I follow a similar development to Claerbout (1999) as
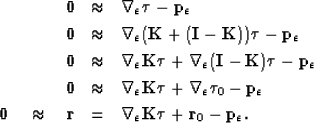
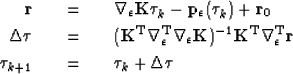
![]() in equation (11) is non-stationary, I solve it using preconditioned conjugate gradients. The preconditioner efficiently exploits Discrete Cosine Transforms(DCTs) to invert a Laplacian operator Lomask and Fomel (2006) as:
in equation (11) is non-stationary, I solve it using preconditioned conjugate gradients. The preconditioner efficiently exploits Discrete Cosine Transforms(DCTs) to invert a Laplacian operator Lomask and Fomel (2006) as:
![\begin{displaymath}
\Delta \boldsymbol{\tau} \approx {\rm DCT_{3D}}^{-1} \left[{...
...abla_\epsilon\it{^{\rm T}}{\bf r} \right]}\ \over { J} \right],\end{displaymath}](img11.gif)
![]() and
and ![]() so that equation (11) becomes
so that equation (11) becomes
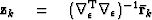 using equation (13)
subtract off reference trace
using equation (13)
subtract off reference trace 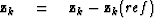 if first iteration {
if first iteration {
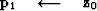 } else{
} else{
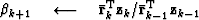
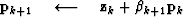 }
}
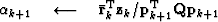
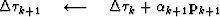
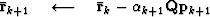 }
}
![]() . This is essentially the average of the divergence of the remaining dips, i.e. ,
. This is essentially the average of the divergence of the remaining dips, i.e. ,