




Next: Impulse responses
Up: Shan: Implicit migration for
Previous: Optimized one-way wave equation
In the approximated dispersion relation (6), replacing Sz and Sx by the partial differential operators
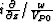 and
and 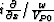 , we obtain a partial differential equation as follows:
, we obtain a partial differential equation as follows:
| 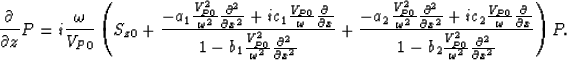 |
(7) |
Equation (7) can be solved by cascading as follows:
| 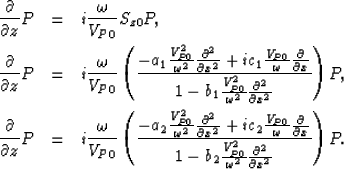 |
(8) |
| (9) |
| (10) |
Equation (8) can be solved by a phase-shift in the space domain.
Let 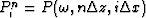 , where
, where 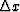 and
and 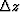 are the grid size of finite-difference scheme.
In equation (9), replacing the partial differential operators by the finite-difference operators as follows:
are the grid size of finite-difference scheme.
In equation (9), replacing the partial differential operators by the finite-difference operators as follows:
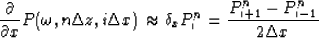
and
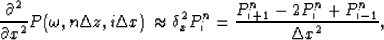
we can derive the following finite difference equation:
| 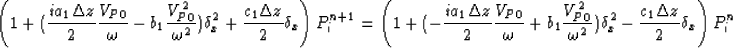 |
(11) |
Fourier analysis shows that the finite-difference scheme (11) is stable. Its computational cost is
almost same as that of the finite-difference scheme for isotropic media. Equation (10) can be solved similarly.





Next: Impulse responses
Up: Shan: Implicit migration for
Previous: Optimized one-way wave equation
Stanford Exploration Project
1/16/2007
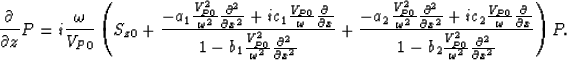
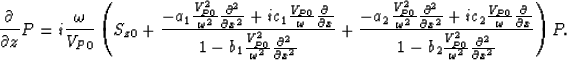
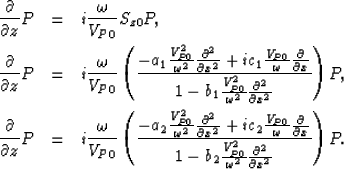
![]()
![]()