




Next: Conclusion
Up: Shan: Implicit migration for
Previous: Finite-difference scheme
Figure 1 shows the impulse responses of the optimized implicit finite-difference method.
The medium is homogeneous, in which the vertical velocity of the medium is 2000 m/s,
the anisotropy parameter  is 0.4, the anisotropy parameter
is 0.4, the anisotropy parameter 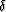 is 0.2 and the tilting angle is
is 0.2 and the tilting angle is
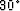 . The travel time of the impulse responses are 0.4s, 0.6s and 0.8s, respectively.
The impulse location is at x=4000m.
For comparison,
I also present the impulse responses of phase-shift (Figure 2) and the impulse responses
of plane-wave migration in tilted coordinates (Figure 3).
Notice in Figure 2, although we use the phase-shift method, we can not achieve
. The travel time of the impulse responses are 0.4s, 0.6s and 0.8s, respectively.
The impulse location is at x=4000m.
For comparison,
I also present the impulse responses of phase-shift (Figure 2) and the impulse responses
of plane-wave migration in tilted coordinates (Figure 3).
Notice in Figure 2, although we use the phase-shift method, we can not achieve 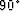 in the right section. The reason is that the waves on the right side overturn when the propagation direction is
close to the horizontal and the phase-shift method is still a one-way equation based method.
Figure 3 shows the impulse responses generated by plane-wave migration in tilted coordinates
Shan and Biondi (2004), which extrapolate the wavefield accurately even when the waves overturn.
Comparing the left section of the impulse responses of Figure 1-3, I find that the
impulse responses of optimized implicit finite-difference is very close to the other two. In the right section in
Figure 1, optimized implicit finite-difference loses accuracy when the waves propagate almost
horizontally or they overturn, since it is still a one-way based method. The impulse responses in Figure
1 have heart-shaped noise, which are typical evanescent energy in implicit finite-difference.
in the right section. The reason is that the waves on the right side overturn when the propagation direction is
close to the horizontal and the phase-shift method is still a one-way equation based method.
Figure 3 shows the impulse responses generated by plane-wave migration in tilted coordinates
Shan and Biondi (2004), which extrapolate the wavefield accurately even when the waves overturn.
Comparing the left section of the impulse responses of Figure 1-3, I find that the
impulse responses of optimized implicit finite-difference is very close to the other two. In the right section in
Figure 1, optimized implicit finite-difference loses accuracy when the waves propagate almost
horizontally or they overturn, since it is still a one-way based method. The impulse responses in Figure
1 have heart-shaped noise, which are typical evanescent energy in implicit finite-difference.





Next: Conclusion
Up: Shan: Implicit migration for
Previous: Finite-difference scheme
Stanford Exploration Project
1/16/2007