




Next: Finite-difference scheme
Up: Shan: Implicit migration for
Previous: Introduction
In a VTI medium, the phase velocity of qP- and qSV-waves in Thomsen's notation
can be expressed as Tsvankin (1996):
| 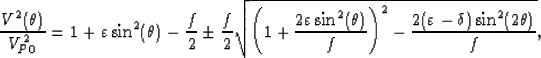 |
(1) |
where 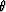 is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0 are the qP- and qSV- wave velocities in the vertical direction, respectively.
is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0 are the qP- and qSV- wave velocities in the vertical direction, respectively.
 and
and 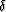 are anisotropy parameters defined by Thomsen (1986):
are anisotropy parameters defined by Thomsen (1986):
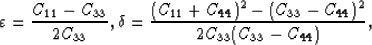
where Cij are elastic moduli.
In equation (1), 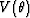 is qP-wave phase-velocity when the sign in front of the square root is positive,
and the qSV-wave phase velocity for a negative sign.
is qP-wave phase-velocity when the sign in front of the square root is positive,
and the qSV-wave phase velocity for a negative sign.
Rotating the symmetry axis from vertical to a tilted angle 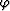 , we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle
, we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle 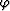 with the vertical direction:
with the vertical direction:
| 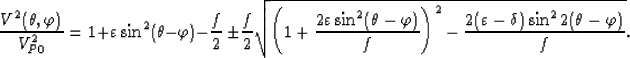 |
(2) |
Here, in contrast to equation (1),  and
and 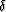 are now defined in a direction tilted by the angle
are now defined in a direction tilted by the angle
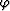 from the vertical direction. VP0 is the qP-wave velocity in the direction parallel to the symmetry axis.
from the vertical direction. VP0 is the qP-wave velocity in the direction parallel to the symmetry axis.
The phase angle 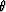 is related to the wavenumbers kx and kz by:
is related to the wavenumbers kx and kz by:
|  |
(3) |
where 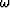 is the temporal frequency. Let
is the temporal frequency. Let 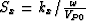 , and
, and 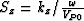 .We can obtain a dispersion relation equation from equations (2) and (3):
.We can obtain a dispersion relation equation from equations (2) and (3):
|
d4Sz4+d3Sz3+d2Sz2+d1Sz+d0=0,
|
(4) |
where the coefficients d0,d1,d2,d3, and d4 are as follows:
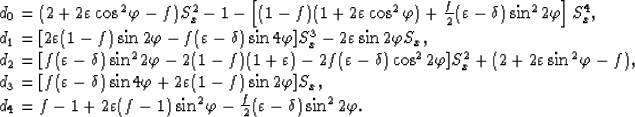
Equation (4) is a quartic equation and there is no explicit expression for its solution.
Generally, the Padé approximation suggests that
if the function 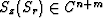 , then Sz(Sr) can be approximated by a rational function
Rn,m(Sr):
, then Sz(Sr) can be approximated by a rational function
Rn,m(Sr):
| 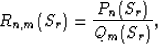 |
(5) |
where
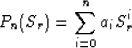
and
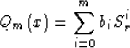
are polynomials of degree n and m, respectively. The coefficients ai and bi can be obtained
either analytically by Taylor-series analysis or numerically by least-squares fitting.
For an isotropic or VTI medium, Sz is an even function of Sx. We can approximate the dispersion
relation with even rational functions, such as Sx2, Sx4.
For TTI media, Sz is not an symmetric function of Sx.
Therefore, in addition to even rational functions, we need odd rational functions to approximate the
dispersion relation, such as Sx, Sx3.
The fourth order approximation for the dispersion relation of TTI media is as follows:
| 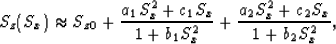 |
(6) |
where Sz0=Sz(0) and the coefficients c1,b1,a1,c2,b2,a2 can be estimated by least-squares methods.
They are functions of
the anisotropy parameters  ,
, 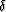 and the tilting angle
and the tilting angle 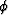 . When these parameters vary
laterally, the coefficients c1,b1,a1,c2,b2,a2 also vary laterally. It is too expensive to
run least-squares estimation for each grid point during the wavefield extrapolation.
They can be calculated and stored in a table before the wavefield extrapolation.
During the wavefield extrapolation, given the anisotropy parameters
. When these parameters vary
laterally, the coefficients c1,b1,a1,c2,b2,a2 also vary laterally. It is too expensive to
run least-squares estimation for each grid point during the wavefield extrapolation.
They can be calculated and stored in a table before the wavefield extrapolation.
During the wavefield extrapolation, given the anisotropy parameters  ,
, 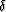 , and the tilting angle
, and the tilting angle 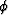 ,
we search for these coefficients from the table and put them into the finite-difference algorithm.
Given the coefficients found from the table,
the finite difference algorithm in TTI media is similar to the isotropic media.
,
we search for these coefficients from the table and put them into the finite-difference algorithm.
Given the coefficients found from the table,
the finite difference algorithm in TTI media is similar to the isotropic media.





Next: Finite-difference scheme
Up: Shan: Implicit migration for
Previous: Introduction
Stanford Exploration Project
1/16/2007
![]()
![]() , we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle
, we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle ![]() with the vertical direction:
with the vertical direction:
![]() is related to the wavenumbers kx and kz by:
is related to the wavenumbers kx and kz by:
![]() , then Sz(Sr) can be approximated by a rational function
Rn,m(Sr):
, then Sz(Sr) can be approximated by a rational function
Rn,m(Sr):
![]()
![]()