Next: Internal precision
Up: R. Clapp: Data precision
Previous: Input data precision
To test the validity of reducing the data precission I simulated a reduced
byte representation by first normalizing the dataset so its maximum
value is one and then using various quantization intervals.
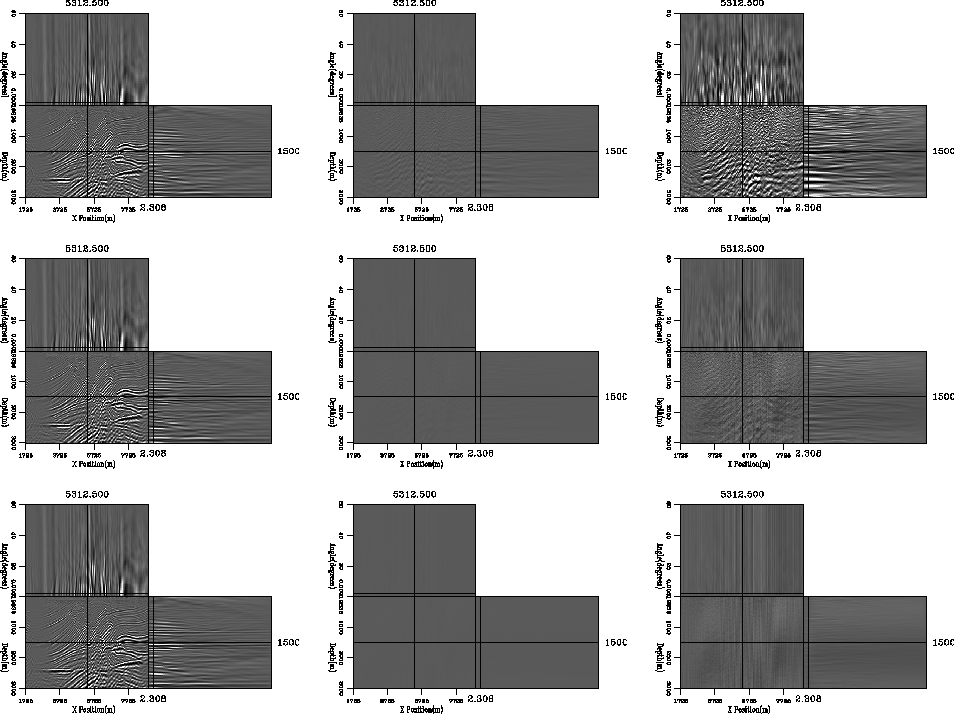
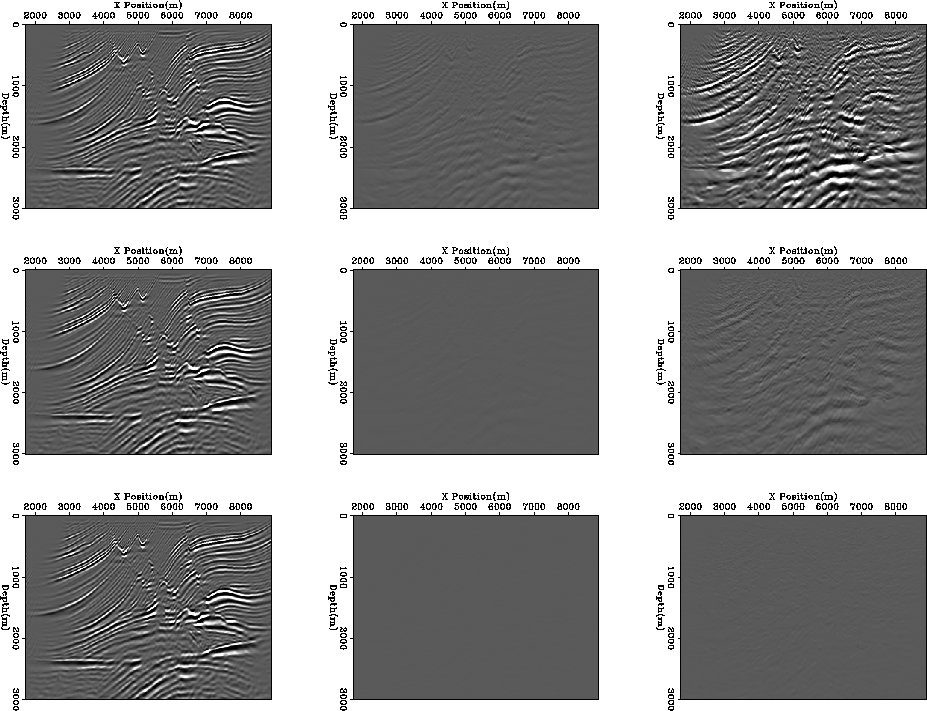
Figure 1 shows three different quantization levels.
The left collumn is the migration result. The center collumn
is the difference between the full precission migration and the reduced precission image
clipped at the same level as the migration.
The right collumn is the same as the center panel but clipped at 1/10 of the value.
The top row is quantizated at .25 (two bits)., the center row at .0625 (four
bits), and the bottom row at .015625 (six bits).
At two bits you can see some very minor differences in structure
and a significant difference in amplitude the quanitized image.
At four bits the error is only noticable at 1/10th the clip, and
at six bits the error has almost completely disapeared.
bitinput
Figure 1
The result of migrating with a reduced precision input.
The left collumn is the migration result. The center collumn
is the difference between the full precission migration and the reduced precission image
clipped at the same level is the migration.
The right collumn is the same as the center panel, clipped at 1/10 the value.
The top row is quantizated at .25 (two bits)., the center row at .0625 (four
bits), and the bottom row at .015625 (six bits).
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





If we assume
that our migration aperture is 200
samples with 50 offsets and 2 non-zero elements in  in time we
get an error reduction of about 140 through the migration process.
The image on the screen is an eight bit representation of the migration
result. The data is clipped at
in time we
get an error reduction of about 140 through the migration process.
The image on the screen is an eight bit representation of the migration
result. The data is clipped at  of the maximum value.
As a result we should need
of the maximum value.
As a result we should need  quantization intervals
without the migration process and a little more than
quantization intervals
without the migration process and a little more than
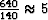 after. Which is confirmed by our test.
Two bits wasn't sufficient four bits was. If we decrease our clip
(right panel) by a factor of ten we should need a little
more than
after. Which is confirmed by our test.
Two bits wasn't sufficient four bits was. If we decrease our clip
(right panel) by a factor of ten we should need a little
more than 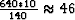 intervals which explains
why the error is elimiated using 6 bits.
intervals which explains
why the error is elimiated using 6 bits.
If we form angle gathers rather than just the zero offset image
we are summing over very few points in the offset space to form
each angle. If we assume each angle is on averge formed from
two offsets we get an error reduction of 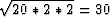 .So an average should take two more bits to form a good angle
domain image. Figure 2 confirms this hypothesis.
The collumns follow the same structure as Figure 1.
The top row is equivalent to 4 bit representation, the center row 6 bit,
and to bottom row 8 bit.
As predicted two more bits are needed. The top panel shows
significant error at the migration clip, the center panel
only shows error at
.So an average should take two more bits to form a good angle
domain image. Figure 2 confirms this hypothesis.
The collumns follow the same structure as Figure 1.
The top row is equivalent to 4 bit representation, the center row 6 bit,
and to bottom row 8 bit.
As predicted two more bits are needed. The top panel shows
significant error at the migration clip, the center panel
only shows error at 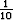 the clip and the bottom
panel shows no meaningful error.
the clip and the bottom
panel shows no meaningful error.
angle
Figure 2
The result of migrating with a reduced precision input.
The left collumn is the migration result. The center collumn
is the difference between the full precission migration and the reduced precission image
clipped at the same level is the migration.
The right collumn is the same as the center panel, clipped at 1/10 the value.
The top row is equivalent to 4 bit representation, the center row 6 bit,
and to bottom row 8 bit.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





For 3-D problems the number of bits that are needed should further
reduce. Instead of summing over 15000 points to form a single image
space in this small 2-D synthetic the number quickly jumps to
more than 10000000, increasing the error reduction factor to
more than 3000 for post-stack images and 300 for prestack images.
As a result even less precision is needed to achieve the same
result. A significant caveat is where to begin the quantization intervals.
In areas with very strong noise (ground roll) or a strong reflector (salt)
a clip before introducing the quantization intervals is a good idea.





Next: Internal precision
Up: R. Clapp: Data precision
Previous: Input data precision
Stanford Exploration Project
1/16/2007
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)