Internal precision

The above sections assumed that the data was automatically converted to a floating point representation throughout the migration process. If you can and want to completely implement your migration on an external hardware device than the initial reduced bit precision is acceptable. The more likely scenario is that part of the migration process will be implemented on the processor and part on an external hardware device. FPGAs, GPUs, and the cell processor excel at certain tasks, but perform quite poorly at others. For example, implementing something that is `if' statetement intensive on an FPGA is not efficient. As a result quantization of the input data alone is not sufficient.

Downward continuing a wavefield in a v(x,z) medium has three basic computational parts that are constantly repeated: multiplication by a correction factor, Fast Fourier Transform (FFT), and multiplication by a complex exponential. At least two, and potentially all three, would be good candidates for an FPGA. Other poritions of the downward continuation process such as managing wavefields to handle multiple reference velocities would be inappropriate. As a result what we need to limit are internal data representation so we can reduce the number of bits that need to be sent to and from the external hardware device. This makes the error analysis of the last section much more complicated.

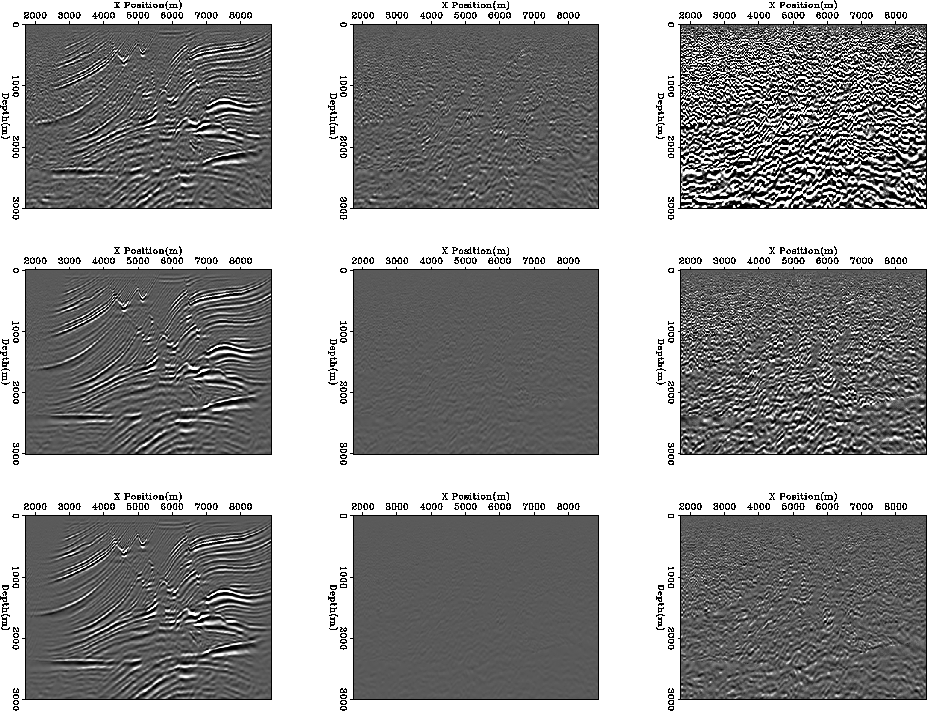
The fact that we only need to produce an image that is accurate to about 1000 quantization intervals gives us some hope. The FFT operation is a series of intergals, so the same error analysis can be performed. We are not summing over a large number of points at every step in the downward continuation process so we will need more precision than before. Figure 3 is the same design as Figures  and 2. The top row simulates six bits, the center 8 bits, and the bottom 9 bits. In this case it takes 9 bits to get the error down to less than 1%.

 

ints
Figure 3 The result of migrating with a reduced precision input. The left collumn is the migration result. The center collumn is the difference between the full precission migration and the reduced precission image clipped at the same level is the migration. The right collumn is the same as the center panel, clipped at 1/10 the value. The top row simulates six bits, the center 8 bits, and the bottom 9 bits.

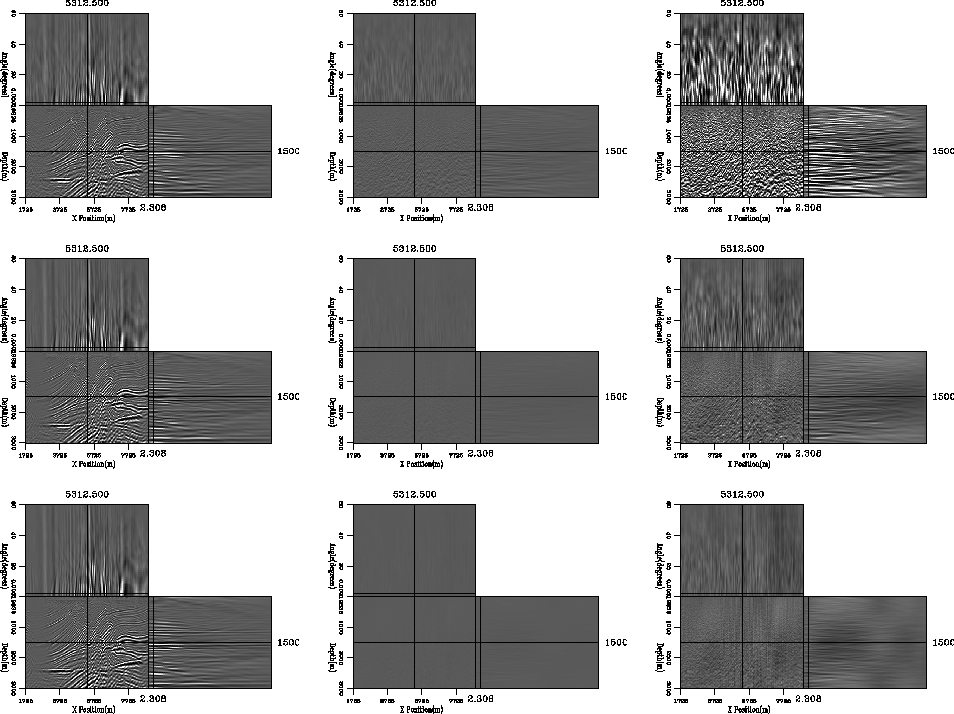
To produce acceptable angle gathers requires significantly more bits. Figure 4 is in the same form as the previous figures. The top row simulates nine bits, the center 11 bits, and the bottom row 12 bits. To get the error below two percent requires a significant bit representation, but for almost all applications the nine bit representation is more than acceptable.

 

ang
Figure 4 The result of migrating with a reduced precision input. The left collumn is the migration result. The center collumn is the difference between the full precission migration and the reduced precission image clipped at the same level is the migration. The right collumn is the same as the center panel, clipped at 1/10 the value. The top row simulates nine bits, the center 11 bits, and the bottom row 12 bits.