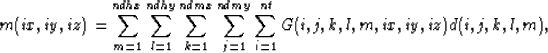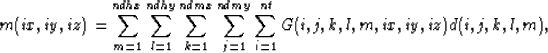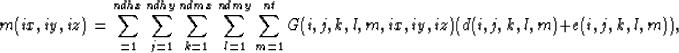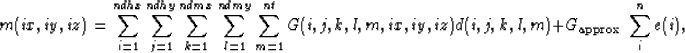Next: Data quantization results
Up: R. Clapp: Data precision
Previous: R. Clapp: Data precision
To understand why we can reduce the precision of our input data
without meaningful loss in final image quality it is important
to remember that migraton is summing along a surface in
multi-dimensional space.
Imagine the process of forming an image m at a given ix,iy, and iz.
To form this one point in image space involves a sumation over a
five-dimensional (t,hx,hy,mx,my) input space of the data
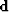 multiplied by the Green's function
multiplied by the Green's function 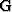 ,
,
| 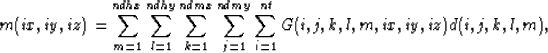 |
(1) |
where ndhx, ndhy, ndmx, ndmy, and nt are the maximum
number of samples of the data in all five dimensions. In reality
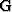 is limited by aperature range in space and only has a few
non-zero elements along the time axis, but still we are summing
over a very large number of points to form a single output location.
is limited by aperature range in space and only has a few
non-zero elements along the time axis, but still we are summing
over a very large number of points to form a single output location.
When we reduce the precision of our data what we are really
doing is introducing an error in each data sample, as a result
Equation(1) becomes
| 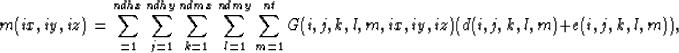 |
(2) |
where e is the error associated with reducing the data precision.
When we reduce the precision we are quantizing
our data. The quantization process is zero mean and has a
standard deviation of 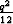 where q is our quantization
interval.
where q is our quantization
interval.
 has relatively low amplitude variation so should not emphasize
the quantization error in any coherent manner.
For this analysis we can think of rewriting
has relatively low amplitude variation so should not emphasize
the quantization error in any coherent manner.
For this analysis we can think of rewriting
Equation (2) as
| 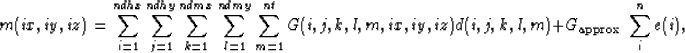 |
(3) |
where n is the number of non-zero elements of 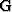 and
and 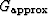 is a scalar with the mean non-zero
value of
is a scalar with the mean non-zero
value of 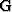 .Most error analysis theory assumes that our errors have
a normal rather than an uniform distribution, so we won't
get quite the same level of error reduction, but generally
the error
.Most error analysis theory assumes that our errors have
a normal rather than an uniform distribution, so we won't
get quite the same level of error reduction, but generally
the error 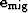 in our migration result by quantizing are data
should be a little higher than
in our migration result by quantizing are data
should be a little higher than
| 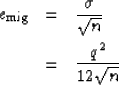 |
|
| (4) |
The size of n is going to depend on what type of problem
we are doing. If we want velocity information, our image
space has an offset or angle axis n will be smaller and
we will have to have a smaller quantization step to obtain
an equivalent image.





Next: Data quantization results
Up: R. Clapp: Data precision
Previous: R. Clapp: Data precision
Stanford Exploration Project
1/16/2007