




Next: Convex Optimization
Up: Witten and Grant: Convex
Previous: Introduction
The Dix equation is a nonlinear relationship between RMS velocity and
interval velocity. It is, however, linear in the square of the interval
velocity. This linearized formulation of the Dix equation was solved by
Clapp et al. (1998) by using a preconditioned least-squares
optimization with spatial smoothness constraints. In this approach
or data fitting goal is to minimize the residual of
| 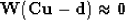 |
(1) |
where 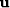 is a vector whose components range over vertical
traveltime depth
is a vector whose components range over vertical
traveltime depth  and whose values are the interval velocity
squared v2int.
and whose values are the interval velocity
squared v2int. 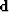 is the data vector which has the same
range as
is the data vector which has the same
range as 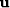 , but whose values are the scaled RMS velocity squared
, but whose values are the scaled RMS velocity squared
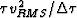 where
where 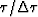 is the index on
the time axis.
is the index on
the time axis. 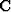 is the casual integration operator. And
is the casual integration operator. And 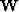 is a weight matrix which is proportional to
our confidence in RMS velocities.
is a weight matrix which is proportional to
our confidence in RMS velocities.
Since the fitting goal, equation 1, is unstable when there are high
frequency variations in RMS velocity, a regularization term is added
to penalize this erratic behavior. As done by
Valenciano et al. (2003), first order derivatives are
used. This system of equations is
| 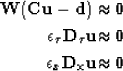 |
|
| |
| (2) |
where 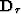 and
and 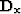 are first-order finite differences
derivatives in traveltime and midpoint, respectively.
are first-order finite differences
derivatives in traveltime and midpoint, respectively.
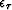 and
and 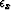 balance the relative importance
of the two model residuals, effectively controlling the smoothness.
balance the relative importance
of the two model residuals, effectively controlling the smoothness.
The approach taken towards the regularization terms will determine
whether a smooth or discontinuous model is found. 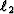 regularization will produce a smooth result. If a discontinuous
velocity is geologically expected, such as for carbonates,
regularization will produce a smooth result. If a discontinuous
velocity is geologically expected, such as for carbonates, 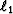 regularization can be used to produce a blocky model Valenciano et al. (2003).
regularization can be used to produce a blocky model Valenciano et al. (2003).





Next: Convex Optimization
Up: Witten and Grant: Convex
Previous: Introduction
Stanford Exploration Project
1/16/2007
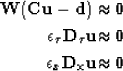
![]() regularization will produce a smooth result. If a discontinuous
velocity is geologically expected, such as for carbonates,
regularization will produce a smooth result. If a discontinuous
velocity is geologically expected, such as for carbonates, ![]() regularization can be used to produce a blocky model Valenciano et al. (2003).
regularization can be used to produce a blocky model Valenciano et al. (2003).