




Next: Least-Squares Dix Equation
Up: Witten and Grant: Convex
Previous: Witten and Grant: Convex
Interval velocity estimation is a fundamental problem in seismology.
The simplest technique for finding interval velocity is the Dix
equation Dix (1952) which analytically inverts the root-mean-square
(RMS) velocity for interval velocity. The Dix equation has many
flaws including the assumption of a vertically stratified earth and
numerical problems that can cause the inversion to become unstable for
rapidly varying velocities. To better constrain the solution, the Dix
equation is often cast as a least-squares problem, which is
regularized in time with a differential operator that penalizes rapid
variations to produce a smooth result Clapp et al. (1998).
Valenciano et al. (2003) expanded on this work to use
both 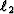 and
and 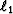 regularization. The
regularization. The 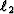 regularization is
justified when the expected velocity model is smooth. When geological
expectations dictate abrupt changes in interval velocity
regularization is
justified when the expected velocity model is smooth. When geological
expectations dictate abrupt changes in interval velocity 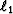 regularization can be utilized to preserve sharp boundaries when they
are present, yet allows for smooth velocity elsewhere.
regularization can be utilized to preserve sharp boundaries when they
are present, yet allows for smooth velocity elsewhere.
Since least-squares problems are already convex, this is a perfect
problem to test the utility of convex optimization. Here we
utilize convex optimization to solve the problem of
interval velocity estimation using the same examples as those present
by Valenciano et al. (2003) for the 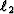 and
and
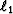 regularization, which used conjugate gradient methods. As well, bounds will
be enforced on the solution to further constrain the Dix inversion to
a more geologically sensible answer.
regularization, which used conjugate gradient methods. As well, bounds will
be enforced on the solution to further constrain the Dix inversion to
a more geologically sensible answer.





Next: Least-Squares Dix Equation
Up: Witten and Grant: Convex
Previous: Witten and Grant: Convex
Stanford Exploration Project
1/16/2007
![]() and
and ![]() regularization. The
regularization. The ![]() regularization is
justified when the expected velocity model is smooth. When geological
expectations dictate abrupt changes in interval velocity
regularization is
justified when the expected velocity model is smooth. When geological
expectations dictate abrupt changes in interval velocity ![]() regularization can be utilized to preserve sharp boundaries when they
are present, yet allows for smooth velocity elsewhere.
regularization can be utilized to preserve sharp boundaries when they
are present, yet allows for smooth velocity elsewhere.
![]() and
and
![]() regularization, which used conjugate gradient methods. As well, bounds will
be enforced on the solution to further constrain the Dix inversion to
a more geologically sensible answer.
regularization, which used conjugate gradient methods. As well, bounds will
be enforced on the solution to further constrain the Dix inversion to
a more geologically sensible answer.