




Next: [3] The scattering potential
Up: wave propagator and its
Previous: [1] Acoustic wave equation
In seismic wave imaging, the scalar wave equation is much more commonly used. Given the Fourier transform of the scalar wave equation for a point source,
| 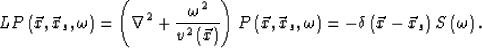 |
(10) |
Equation (10) is a Helmholtz equation. Here 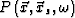 is a total pressure field,
is a total pressure field, 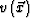 is the variable acoustic velocity, the density is assumed to be constant, and
is the variable acoustic velocity, the density is assumed to be constant, and 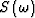 is a source function.
Taking an initial estimation of the medium velocity,
is a source function.
Taking an initial estimation of the medium velocity, 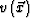 , as the background velocity
, as the background velocity 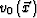 ,
, 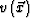 can be split into the known and unknown parts by the following:
can be split into the known and unknown parts by the following:
| 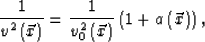 |
(11) |
where the background velocity 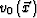 need not be constant. The variable
need not be constant. The variable 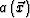 is the unknown velocity perturbation to be determined from the data, which is called the scattering potential of the medium, since it is a measure of the scattering strength at points where the actual medium differs from the background medium. Substituting equation (11) into equation (10) yields
is the unknown velocity perturbation to be determined from the data, which is called the scattering potential of the medium, since it is a measure of the scattering strength at points where the actual medium differs from the background medium. Substituting equation (11) into equation (10) yields
| 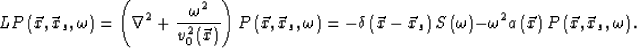 |
(12) |
For the background medium, the background Green's function satisfies the following equation:
| 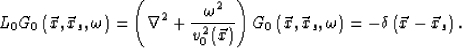 |
(13) |
Therefore, with the help of the Lippman-Schwinger equation of equation (3), the total pressure wave is
| 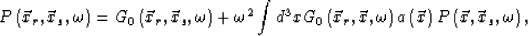 |
(14) |
and the scattering wave field caused by the scattering potential 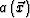 is
is
| 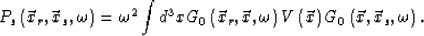 |
(15) |
Equations (9) and (15) create a link between the scattered wavefield and the scattering potentials. They are Fredholm integral equations of the first kind and are the bases of the linearized inversion. Given the observed scattered wavefield, the scattering potentials can be solved.





Next: [3] The scattering potential
Up: wave propagator and its
Previous: [1] Acoustic wave equation
Stanford Exploration Project
11/1/2005