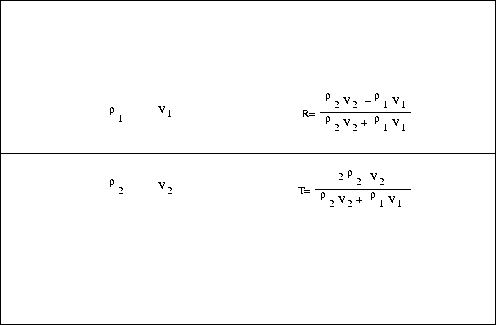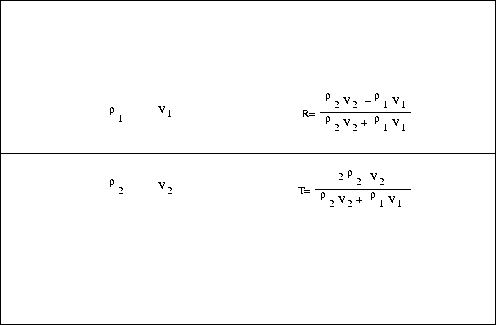[3] The scattering potential and the reflectivity

 

reflectivity
Figure 1 The acoustic wave reflectivity and the transmission of a planar reflector in the case of zero incident angle

From Fig.1, and assuming that the density is constant, the normal reflectivity is defined as  

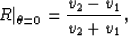$$R\vert_{\theta =0} = \frac{v_{2}-v_{1}}{v_{2}+v_{1}},$$ (16)

and the transmission coefficient is  

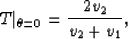$$T\vert_{\theta =0} = \frac{2v_{2}}{v_{2}+v_{1}},$$ (17)

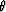where $\theta$ is the incident angle. Therefore, defining the scattering potential as 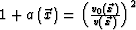$1+a\left( \vec{x}\right)=\left(\frac{v_{0}\left( \vec{x}\right)}{v\left( \vec{x}\right)} \right) ^{2}$, equation (16) and (17) can be rewritten as  

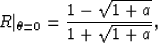$$R\vert_{\theta =0}=\frac{1-\sqrt{1+a}}{1+\sqrt{1+a}},$$ (18)

and  

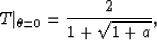$$T\vert_{\theta =0}=\frac{2}{1+\sqrt{1+a}},$$ (19)

respectively. If waves meet a reflector with a non-zero incident angle, the reflectivity and transmission coefficient are  

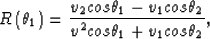$$R\left( \theta_{1}\right) = \frac{v_{2}cos\theta _{1}-v_{1}cos\theta _{2}}{v^{2}cos\theta_{1}+v_{1}cos\theta _{2}},$$ (20)

and  

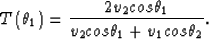$$T\left( \theta_{1}\right) = \frac{2v_{2}cos\theta _{1}}{v_{2}cos\theta _{1}+v_{1}cos \theta _{2}}.$$ (21)

Similarly, they can be expressed with the scattering potential as  

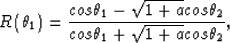$$R\left( \theta_{1}\right)=\frac{cos\theta_{1}-\sqrt{1+a}cos\theta _{2}}{cos\theta_{1}+\sqrt{1+a}cos\theta_{2}},$$ (22)

and  

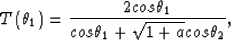$$T\left( \theta_{1}\right)=\frac{2cos\theta_{1}}{cos\theta _{1}+\sqrt{1+a}cos\theta _{2}},$$ (23)

respectively. The angle reflectivity has a close relation to the scattering potentials. Generally, the angle reflectivity is estimated by amplitude-preserved imaging, and lithological parameter disturbances are evaluated from them by AVO/AVA inversion.