




Next: Dipping water-bottom
Up: Flat water-bottom
Previous: Non-diffracted multiple
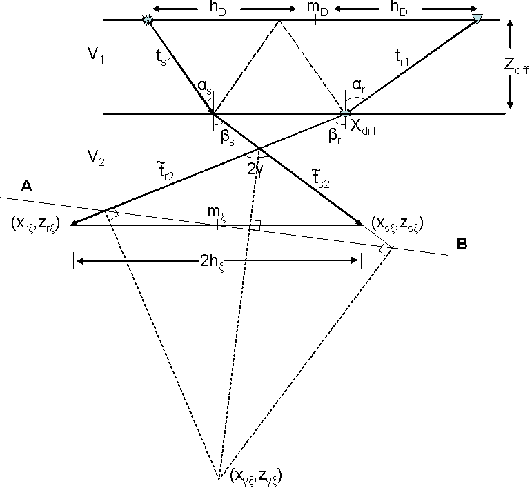
Consider now a diffractor sitting at the water-bottom as illustrated in the
sketch in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The source- and receiver-side multiples
are described by equations 2-4
as did the water-bottom multiple.
In this case, however, the take-off angles from source and receiver
are different even if the surface offset is the same as that in
Figure
. The source- and receiver-side multiples
are described by equations 2-4
as did the water-bottom multiple.
In this case, however, the take-off angles from source and receiver
are different even if the surface offset is the same as that in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In fact, since the reflection is non-specular
at the location of the diffractor, Xdiff needs to be known
in order for the receiver take-off angle to be computed. The traveltime
of the diffracted multiple is given by
. In fact, since the reflection is non-specular
at the location of the diffractor, Xdiff needs to be known
in order for the receiver take-off angle to be computed. The traveltime
of the diffracted multiple is given by
| ![\begin{displaymath}
t_m=\frac{1}{V_1}\left[3\sqrt{Z_{wb}^2+\left[\frac{X_{diff}-...
...t]^2}+\sqrt{\left[(m_D+h_D)-X_{diff}\right]^2+Z_{wb}^2}\right],\end{displaymath}](img54.gif) |
(21) |
where Zwb=Zdiff can be computed from the traveltime of the multiple
for the zero subsurface offset trace (tm(0)) by solving the quadratic
equation in Zwb2 that results from setting hD=0 in
equation 21:
|
64Zwb4-20V12tm2(0)Zwb2+(V14tm4(0)-4V12tm2(0)(mD-Xdiff)2)=0
|
(22) |
mul_sktch5
Figure 7 Imaging of receiver-side diffracted
water-bottom multiple from a diffractor sitting on top of a flat water-bottom.
At the diffractor the reflection is non-specular.
Notice that 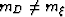 . . |
|  |

The coordinates of the image point, according to
equations 2-4 are given by
| 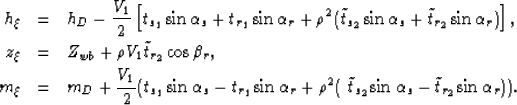 |
(23) |
| (24) |
| (25) |
The traveltimes of the individual ray segments are given by
| 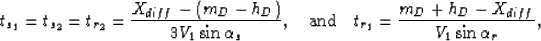 |
(26) |
whereas the traveltimes of the refracted rays can be computed
from equation 5:
| 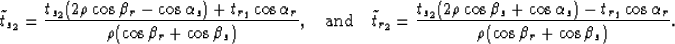 |
(27) |
where, according to equations 9 and 10:
| 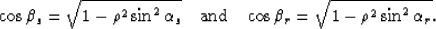 |
(28) |
In order to express 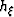 ,
, 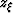 and
and 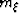 entirely in terms of the
data space coordinates,
all we need to do is compute the sines and cosines of
entirely in terms of the
data space coordinates,
all we need to do is compute the sines and cosines of 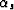 and
and
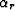 which can be easily done from the sketch of
Figure
which can be easily done from the sketch of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:
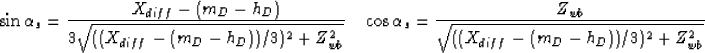

Notice that the diffraction multiple does not migrate as a primary even if
migrated with water velocity. In other words, even if 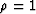 ,
, 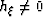 .The only exception is when Xdiff=mD+hD/2 since then the
diffractor is in the right place to make a specular reflection and therefore is
indistinguishable from a non-diffracted water-bottom multiple. In that case,
.The only exception is when Xdiff=mD+hD/2 since then the
diffractor is in the right place to make a specular reflection and therefore is
indistinguishable from a non-diffracted water-bottom multiple. In that case,
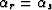 (which in turn implies
(which in turn implies 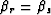 ) and from
equations 5 and 6,
) and from
equations 5 and 6,
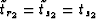 and therefore
equations 23-25 reduce to
equations 14-16, respectively.
image2
and therefore
equations 23-25 reduce to
equations 14-16, respectively.
image2
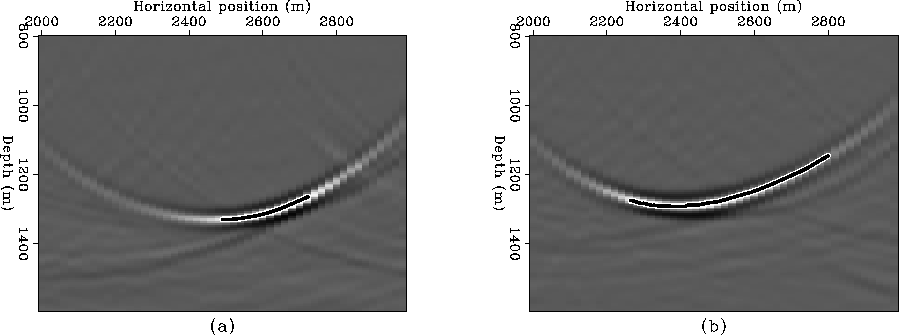
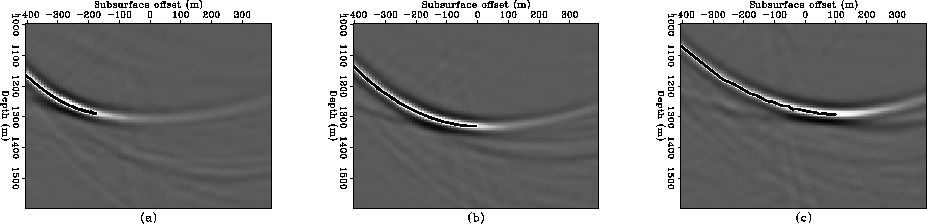
Figure 8 image sections at 0 and -400 m
subsurface offset for a diffracted multiple from a flat water-bottom. The
depth of the water-bottom is 500 m and the diffractor is located at 2500 m.
The solid line represents image reflector computed with
equations 24 and 25.





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two subsurface-offset sections of a
migrated diffracted multiple from a diffractor sitting on top of a flat
reflector as in the schematic of Figure
shows two subsurface-offset sections of a
migrated diffracted multiple from a diffractor sitting on top of a flat
reflector as in the schematic of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The diffractor
position is Xdiff=2,500 m, the CMP range is from 2,000 m to 3,000 m, the
offsets range from 0 to 2,000 m and the water depth is 500 m. The data were
migrated with the same two-layer model described before.
Panel (a) corresponds to zero subsurface offset (
.
The diffractor
position is Xdiff=2,500 m, the CMP range is from 2,000 m to 3,000 m, the
offsets range from 0 to 2,000 m and the water depth is 500 m. The data were
migrated with the same two-layer model described before.
Panel (a) corresponds to zero subsurface offset (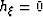 ) whereas panel (b)
corresponds to subsurface offset of -400 m. Overlaid are the residual
moveout curves computed with equations 24 and 25.
Obviously, the zero subsurface offset section is not a good image of the
water-bottom or the diffractor.
) whereas panel (b)
corresponds to subsurface offset of -400 m. Overlaid are the residual
moveout curves computed with equations 24 and 25.
Obviously, the zero subsurface offset section is not a good image of the
water-bottom or the diffractor.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows three SODCIGs taken at locations 2,300 m,
2,500 m and 2,700 m. Unlike the non-diffracted multiple, this time energy
maps to positive or negative subsurface offset depending on the relative
position of the CMP with respect to the diffractor.
In ADCIGs the aperture angle is given by equation 11 which, given
the geometry of Figure
shows three SODCIGs taken at locations 2,300 m,
2,500 m and 2,700 m. Unlike the non-diffracted multiple, this time energy
maps to positive or negative subsurface offset depending on the relative
position of the CMP with respect to the diffractor.
In ADCIGs the aperture angle is given by equation 11 which, given
the geometry of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , reduces to
, reduces to
| ![\begin{displaymath}
\gamma=\frac{1}{2}\sin^{-1}\left[\beta_s+\beta_r\right]=\fra...
...\alpha_s}+\rho\sin\alpha_s\sqrt{1-\rho^2\sin^2\alpha_r}\right].\end{displaymath}](img66.gif) |
(29) |
The depth of the image is given by equation 12,
| ![\begin{displaymath}
z_{\xi_\gamma}=z_\xi-h_\xi\tan\left(\frac{1}{2}\sin^{-1}\lef...
...s}+\rho\sin\alpha_s\sqrt{1-\rho^2\sin^2\alpha_r}\right]\right).\end{displaymath}](img67.gif) |
(30) |
odcig2
Figure 9 SODCIGs from a diffracted multiple from
a flat water-bottom at locations 2,300 m, 2,500 m and 2,700 m.
The diffractor is at 2,500 m. The overlaid residual moveout curves were
computed with equations 23 and 24.





Again, this equation shows that the diffracted multiple is not migrated as a
primary even if 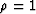 (except in the trivial case Xdiff=mD+hD/2
discussed before for which, since
(except in the trivial case Xdiff=mD+hD/2
discussed before for which, since 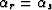 ,
, 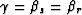 in agreement with equation 19 and so equation 30
reduces to equation 20).
in agreement with equation 19 and so equation 30
reduces to equation 20).
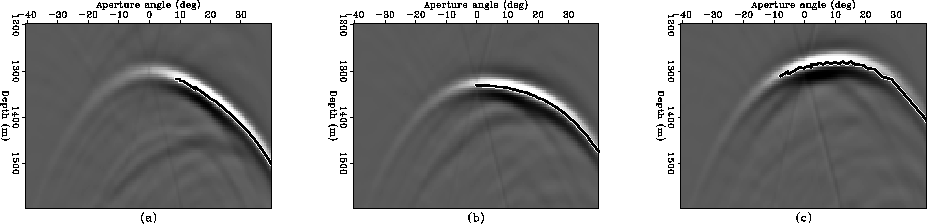
adcig2
Figure 10 ADCIGs corresponding to the SODCIGs
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The overlaid curves are the residual moveout
curves computed with equations 24 and 30.
. The overlaid curves are the residual moveout
curves computed with equations 24 and 30.





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the angle gathers corresponding to the SODCIGs
of Figure
shows the angle gathers corresponding to the SODCIGs
of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice the shift in the apex of the
moveout curves.
. Notice the shift in the apex of the
moveout curves.





Next: Dipping water-bottom
Up: Flat water-bottom
Previous: Non-diffracted multiple
Stanford Exploration Project
11/1/2005
![\begin{displaymath}
t_m=\frac{1}{V_1}\left[3\sqrt{Z_{wb}^2+\left[\frac{X_{diff}-...
...t]^2}+\sqrt{\left[(m_D+h_D)-X_{diff}\right]^2+Z_{wb}^2}\right],\end{displaymath}](img54.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The source- and receiver-side multiples
are described by equations 2-4
as did the water-bottom multiple.
In this case, however, the take-off angles from source and receiver
are different even if the surface offset is the same as that in
Figure
. The source- and receiver-side multiples
are described by equations 2-4
as did the water-bottom multiple.
In this case, however, the take-off angles from source and receiver
are different even if the surface offset is the same as that in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In fact, since the reflection is non-specular
at the location of the diffractor, Xdiff needs to be known
in order for the receiver take-off angle to be computed. The traveltime
of the diffracted multiple is given by
. In fact, since the reflection is non-specular
at the location of the diffractor, Xdiff needs to be known
in order for the receiver take-off angle to be computed. The traveltime
of the diffracted multiple is given by
![\begin{displaymath}
t_m=\frac{1}{V_1}\left[3\sqrt{Z_{wb}^2+\left[\frac{X_{diff}-...
...t]^2}+\sqrt{\left[(m_D+h_D)-X_{diff}\right]^2+Z_{wb}^2}\right],\end{displaymath}](img54.gif)

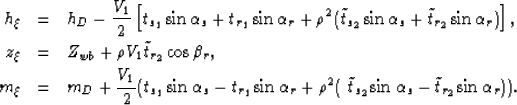
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:
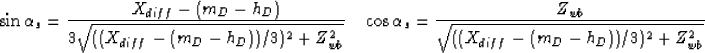

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two subsurface-offset sections of a
migrated diffracted multiple from a diffractor sitting on top of a flat
reflector as in the schematic of Figure
shows two subsurface-offset sections of a
migrated diffracted multiple from a diffractor sitting on top of a flat
reflector as in the schematic of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The diffractor
position is Xdiff=2,500 m, the CMP range is from 2,000 m to 3,000 m, the
offsets range from 0 to 2,000 m and the water depth is 500 m. The data were
migrated with the same two-layer model described before.
Panel (a) corresponds to zero subsurface offset (
.
The diffractor
position is Xdiff=2,500 m, the CMP range is from 2,000 m to 3,000 m, the
offsets range from 0 to 2,000 m and the water depth is 500 m. The data were
migrated with the same two-layer model described before.
Panel (a) corresponds to zero subsurface offset (![]() ) whereas panel (b)
corresponds to subsurface offset of -400 m. Overlaid are the residual
moveout curves computed with equations 24 and 25.
Obviously, the zero subsurface offset section is not a good image of the
water-bottom or the diffractor.
) whereas panel (b)
corresponds to subsurface offset of -400 m. Overlaid are the residual
moveout curves computed with equations 24 and 25.
Obviously, the zero subsurface offset section is not a good image of the
water-bottom or the diffractor.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows three SODCIGs taken at locations 2,300 m,
2,500 m and 2,700 m. Unlike the non-diffracted multiple, this time energy
maps to positive or negative subsurface offset depending on the relative
position of the CMP with respect to the diffractor.
In ADCIGs the aperture angle is given by equation 11 which, given
the geometry of Figure
shows three SODCIGs taken at locations 2,300 m,
2,500 m and 2,700 m. Unlike the non-diffracted multiple, this time energy
maps to positive or negative subsurface offset depending on the relative
position of the CMP with respect to the diffractor.
In ADCIGs the aperture angle is given by equation 11 which, given
the geometry of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , reduces to
, reduces to
![]() (except in the trivial case Xdiff=mD+hD/2
discussed before for which, since
(except in the trivial case Xdiff=mD+hD/2
discussed before for which, since ![]() ,
, ![]() in agreement with equation 19 and so equation 30
reduces to equation 20).
in agreement with equation 19 and so equation 30
reduces to equation 20).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The overlaid curves are the residual moveout
curves computed with equations 24 and 30.
. The overlaid curves are the residual moveout
curves computed with equations 24 and 30.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the angle gathers corresponding to the SODCIGs
of Figure
shows the angle gathers corresponding to the SODCIGs
of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice the shift in the apex of the
moveout curves.
. Notice the shift in the apex of the
moveout curves.