




Next: Diffracted multiple
Up: Flat water-bottom
Previous: Flat water-bottom
The traveltime of the water-bottom multiple is given by
Alvarez (2005)
| 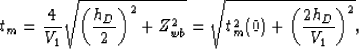 |
(13) |
which is simply the traveltime of a primary at twice the depth of the
water-bottom 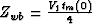 .
.
mul_sktch4
Figure 4 Imaging of water-bottom multiple
for a flat water-bottom. Notice that 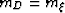 and that the apparent
reflector at the image point is flat. and that the apparent
reflector at the image point is flat.
|
| 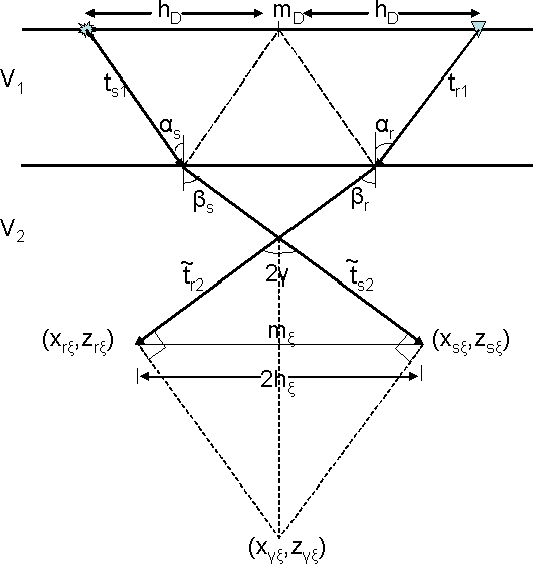 |

From Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) it is clear that due to the symmetry of the
problem, ts1=ts2=tr1=tr2=tm/4 and
it is clear that due to the symmetry of the
problem, ts1=ts2=tr1=tr2=tm/4 and 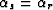 ,
which in turn means
,
which in turn means 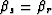 . Furthermore, from
Equations 5 and 6 it immediately follows that
. Furthermore, from
Equations 5 and 6 it immediately follows that
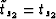 and
and 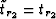 which says that
the traveltimes of the refracted rays are equal to the corresponding
traveltimes of the multiple. Equation 2 thus simplifies to
which says that
the traveltimes of the refracted rays are equal to the corresponding
traveltimes of the multiple. Equation 2 thus simplifies to
| 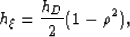 |
(14) |
which indicates that the subsurface offset at the image point of a trace
with half surface offset hD depends only on the velocity contrast
between the water and the sediments. In particular, if the trace is
migrated with the water velocity, i.e. 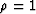 , then
, then 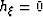 which proves
the claim that the trace is imaged exactly as a primary since it
is mapped to zero subsurface offset irrespective of its surface offset.
It should also be noted that, since usually sediment velocity is faster than
water velocity, then
which proves
the claim that the trace is imaged exactly as a primary since it
is mapped to zero subsurface offset irrespective of its surface offset.
It should also be noted that, since usually sediment velocity is faster than
water velocity, then 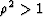 and therefore the multiples are
mapped to subsurface offsets with the opposite sign with respect
to the sign of the surface offset hD when migrated with sediment velocity.
and therefore the multiples are
mapped to subsurface offsets with the opposite sign with respect
to the sign of the surface offset hD when migrated with sediment velocity.
From Equation 3, the depth of the image point can be easily
computed as
| 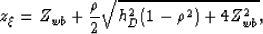 |
(15) |
which for migration with the water velocity reduces to 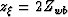 ,which shows that the multiple is migrated as a primary at twice
the water depth. Finally, from Equation 4, the horizontal
position of the image point reduces to
,which shows that the multiple is migrated as a primary at twice
the water depth. Finally, from Equation 4, the horizontal
position of the image point reduces to
| 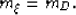 |
(16) |
This result shows that the multiple is mapped in the image space
to the same horizontal position as the corresponding CMP even if
migrated with sediment velocity. This result is obviously a direct
consequence of the symmetry of the raypaths of the multiple reflection in this
case.
Equations 14-16 give the image
space coordinates in terms of the data space coordinates. An important
issue is the functional relationship between the subsurface
offset and the image depth, since it determines the moveout of the
multiples in the subsurface-offset-domain common-image-gathers (SODCIGs).
Replacing 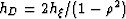 and
and 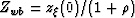 in
Equation 15 we get
in
Equation 15 we get
| 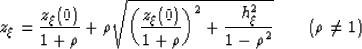 |
(17) |
which shows that the moveout is an hyperbola (actually half of an hyperbola
since we already established that 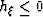 if
if 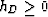 ).
).
odcig1
Figure 5 Subsurface offset domain common
image gather of a water-bottom multiple from a flat water-bottom. Water
velocity is 1500 m/s, water depth 500 m, sediment velocity 2500 m/s and
surface offsets from 0 to 2000 m. Overlaid is the residual moveout curve
computed with Equation 17.
|
| 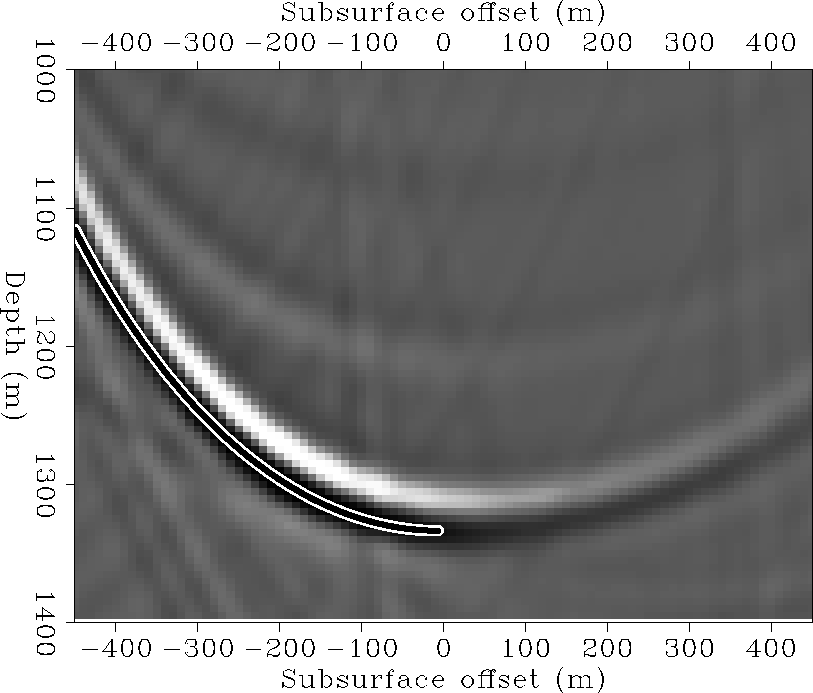 |





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
an SODCIG for a non-diffracted water-bottom multiple from a flat
water-bottom 500 m deep. The data was migrated with a two-layer
velocity model: the water
layer of 1500 m/s and a sediment layer of velocity 2500 m/s. Larger
subsurface offsets (which according to Equation 14 correspond to
larger surface offsets) map to shallower depths (for the normal situation of
shows
an SODCIG for a non-diffracted water-bottom multiple from a flat
water-bottom 500 m deep. The data was migrated with a two-layer
velocity model: the water
layer of 1500 m/s and a sediment layer of velocity 2500 m/s. Larger
subsurface offsets (which according to Equation 14 correspond to
larger surface offsets) map to shallower depths (for the normal situation of
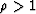 ), as we should expect since the rays are refracted to increasingly
larger angles until the critical reflection angle is reached. Also notice that the hyperbola is shifted down by a factor
), as we should expect since the rays are refracted to increasingly
larger angles until the critical reflection angle is reached. Also notice that the hyperbola is shifted down by a factor 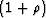 with respect to
the image point when migrated with water velocity.
with respect to
the image point when migrated with water velocity.
In angle-domain common-image-gathers (ADCIGs), the half-aperture angle
reduces to 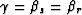 , which in terms of the data
space coordinates is given by
, which in terms of the data
space coordinates is given by
| ![\begin{displaymath}
\gamma=\sin^{-1}\left[\frac{2\rho h_D}{V_1t_m}\right].\end{displaymath}](img46.gif) |
(18) |
The depth of the image can be easily computed from Equation 12.
In particular, if the data are migrated with the velocity of the water,
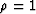 , and therefore
, and therefore 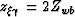 which means a horizontal
line in the (
which means a horizontal
line in the (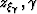 ) plane. Equivalently, we can say that the
residual moveout in the (
) plane. Equivalently, we can say that the
residual moveout in the (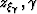 ) plane is zero, once again
corroborating that the water-bottom multiple is migrated as a primary if
) plane is zero, once again
corroborating that the water-bottom multiple is migrated as a primary if
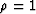 .
Equation 12 can be expressed in terms of the data space coordinates
using Equations 14 and 15 and noting that
.
Equation 12 can be expressed in terms of the data space coordinates
using Equations 14 and 15 and noting that
| 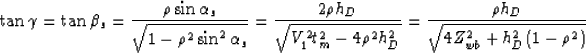 |
(19) |
If 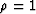 this expression simplifies to
this expression simplifies to 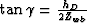 ,
which is the aperture angle of a primary at twice the water-bottom depth.
,
which is the aperture angle of a primary at twice the water-bottom depth.
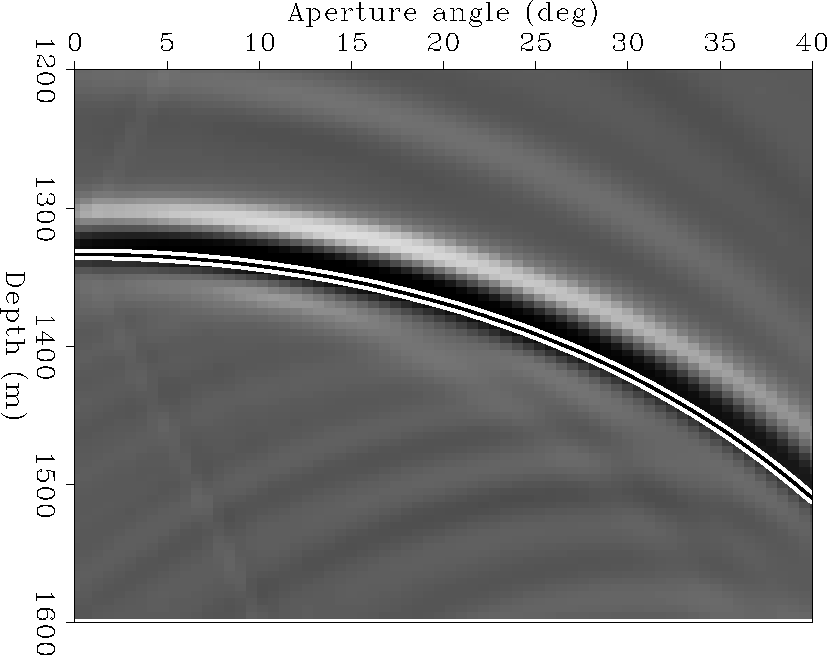
adcig1
Figure 6 Angle domain common
image gather corresponding to the SODCIG shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Overlaid is the residual moveout curve computed with equation 20. .
Overlaid is the residual moveout curve computed with equation 20.
|
|  |





As we did with the SODCIG, it is important to find the functional
relationship between 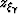 and
and 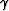 since it dictates the
residual moveout of the multiple in the ADCIG. Plugging
Equations 14 and 15 into equation 12,
using Equations 13, and 18 to eliminate hD and
simplifying we get
since it dictates the
residual moveout of the multiple in the ADCIG. Plugging
Equations 14 and 15 into equation 12,
using Equations 13, and 18 to eliminate hD and
simplifying we get
| ![\begin{displaymath}
z_{\xi_\gamma}=Z_{wb}\left[1+\frac{\cos\gamma(\rho^2-\tan^2\...
...^2-\tan^2\gamma(1-\rho^2))}{\sqrt{\rho^2-\sin^2\gamma}}\right].\end{displaymath}](img52.gif) |
(20) |
Once again, when the multiple is migrated with the water velocity (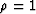 )we get the expected result
)we get the expected result 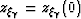 , that is, flat
moveout (no angular dependence).
Figure
, that is, flat
moveout (no angular dependence).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIG corresponding to the SODCIG shown
in Figure
shows the ADCIG corresponding to the SODCIG shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice that the migrated depth at zero aperture
angle is the same as that for zero sub-surface offset in
Figure
. Notice that the migrated depth at zero aperture
angle is the same as that for zero sub-surface offset in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . For larger aperture angles, however, the migrated
depth increases as indicated in equation 20 and as seen in the
schematic of Figure
. For larger aperture angles, however, the migrated
depth increases as indicated in equation 20 and as seen in the
schematic of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.





Next: Diffracted multiple
Up: Flat water-bottom
Previous: Flat water-bottom
Stanford Exploration Project
11/1/2005
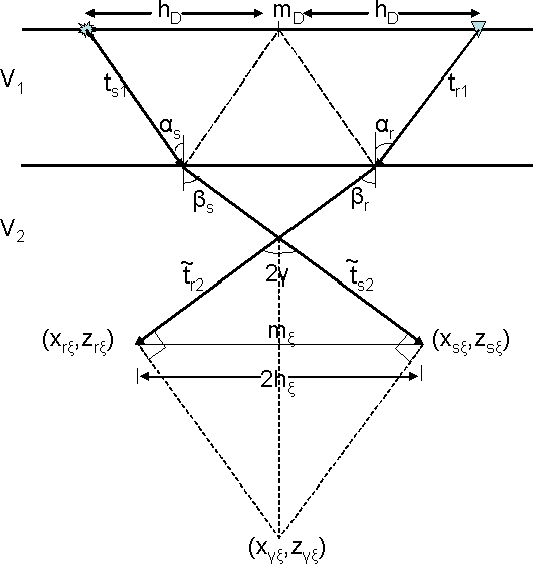
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) it is clear that due to the symmetry of the
problem, ts1=ts2=tr1=tr2=tm/4 and
it is clear that due to the symmetry of the
problem, ts1=ts2=tr1=tr2=tm/4 and ![]() ,
which in turn means
,
which in turn means ![]() . Furthermore, from
Equations 5 and 6 it immediately follows that
. Furthermore, from
Equations 5 and 6 it immediately follows that
![]() and
and ![]() which says that
the traveltimes of the refracted rays are equal to the corresponding
traveltimes of the multiple. Equation 2 thus simplifies to
which says that
the traveltimes of the refracted rays are equal to the corresponding
traveltimes of the multiple. Equation 2 thus simplifies to
![]() and
and ![]() in
Equation 15 we get
in
Equation 15 we get

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
an SODCIG for a non-diffracted water-bottom multiple from a flat
water-bottom 500 m deep. The data was migrated with a two-layer
velocity model: the water
layer of 1500 m/s and a sediment layer of velocity 2500 m/s. Larger
subsurface offsets (which according to Equation 14 correspond to
larger surface offsets) map to shallower depths (for the normal situation of
shows
an SODCIG for a non-diffracted water-bottom multiple from a flat
water-bottom 500 m deep. The data was migrated with a two-layer
velocity model: the water
layer of 1500 m/s and a sediment layer of velocity 2500 m/s. Larger
subsurface offsets (which according to Equation 14 correspond to
larger surface offsets) map to shallower depths (for the normal situation of
![]() ), as we should expect since the rays are refracted to increasingly
larger angles until the critical reflection angle is reached. Also notice that the hyperbola is shifted down by a factor
), as we should expect since the rays are refracted to increasingly
larger angles until the critical reflection angle is reached. Also notice that the hyperbola is shifted down by a factor ![]() with respect to
the image point when migrated with water velocity.
with respect to
the image point when migrated with water velocity.
![]() , which in terms of the data
space coordinates is given by
, which in terms of the data
space coordinates is given by
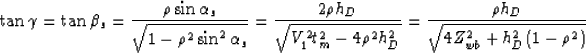
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Overlaid is the residual moveout curve computed with equation 20.
.
Overlaid is the residual moveout curve computed with equation 20.

![]() and
and ![]() since it dictates the
residual moveout of the multiple in the ADCIG. Plugging
Equations 14 and 15 into equation 12,
using Equations 13, and 18 to eliminate hD and
simplifying we get
since it dictates the
residual moveout of the multiple in the ADCIG. Plugging
Equations 14 and 15 into equation 12,
using Equations 13, and 18 to eliminate hD and
simplifying we get
![\begin{displaymath}
z_{\xi_\gamma}=Z_{wb}\left[1+\frac{\cos\gamma(\rho^2-\tan^2\...
...^2-\tan^2\gamma(1-\rho^2))}{\sqrt{\rho^2-\sin^2\gamma}}\right].\end{displaymath}](img52.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIG corresponding to the SODCIG shown
in Figure
shows the ADCIG corresponding to the SODCIG shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice that the migrated depth at zero aperture
angle is the same as that for zero sub-surface offset in
Figure
. Notice that the migrated depth at zero aperture
angle is the same as that for zero sub-surface offset in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . For larger aperture angles, however, the migrated
depth increases as indicated in equation 20 and as seen in the
schematic of Figure
. For larger aperture angles, however, the migrated
depth increases as indicated in equation 20 and as seen in the
schematic of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.