




Next: Application to the isotropic
Up: Biondi: Anisotropic ADCIGs
Previous: Conversion from average angles
In this appendix I derive the expressions for evaluating
the derivatives of image depth 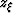 with respect to
the subsurface offset
with respect to
the subsurface offset 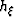 and
the midpoint
and
the midpoint 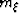 ;these derivatives are computed along the tangent plane to the
impulse response of the generalized migration operator,
which is defined in equations 18-24.
;these derivatives are computed along the tangent plane to the
impulse response of the generalized migration operator,
which is defined in equations 18-24.
I start by deriving the equation for the vector normal to the
impulse-response surface,
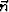 :
:
where
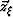 ,
, 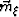 , and
, and 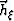 are respectively the unit vectors
along the three dimensions
are respectively the unit vectors
along the three dimensions
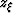 ,
, 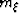 , and
, and 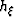 .
.
The equation of the tangent plane at the
image point with coordinates
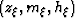 is given by:
is given by:
| 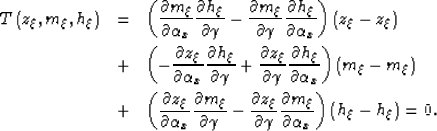 |
|
| |
| (32) |
The derivative of the depth with respect o the subsurface offset,
at constant midpoint, is given by:
| 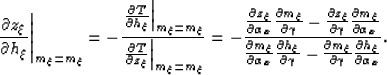 |
(33) |
and similarly the derivative of the depth with respect to the midpoint,
at constant subsurface offset, is given by:
| 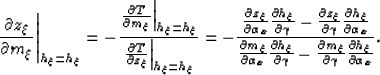 |
(34) |
To evaluate
equations 33-34.
we need to evaluate the following partial derivatives,
obtained by differentiating the expressions in
equations 18-20:
| 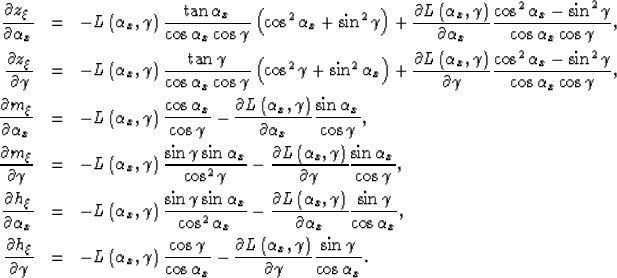 |
|
| |
| |
| |
| |
| (35) |
The derivative of path length are evaluated as follows:
| ![\begin{eqnarray}
&
\frac{\partial L}{\partial \alpha_x}
=
\frac{-t_{D}}
{\left[\...
...frac{\left(S_r-S_s\right)\tan \gamma}{\cos ^2 \alpha_x}
\right],
&\end{eqnarray}](img81.gif) |
|
| (36) |
and
| ![\begin{eqnarray}
&
\frac{\partial L}{\partial \gamma}
=
\frac{-t_{D}}
{\left[\le...
...frac{\left(S_r-S_s\right)\tan \alpha_x}{\cos ^2 \gamma}
\right].
&\end{eqnarray}](img82.gif) |
|
| (37) |
![]() :
:
![]() is given by:
is given by:
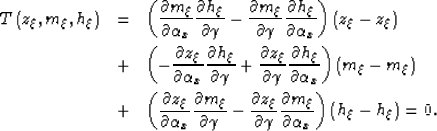
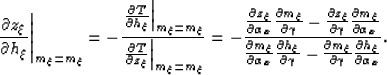
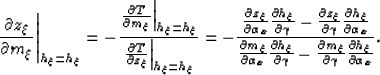
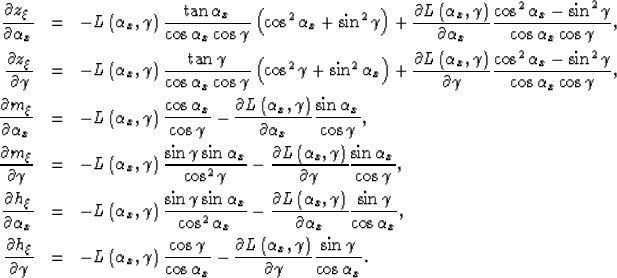
![\begin{eqnarray}
&
\frac{\partial L}{\partial \alpha_x}
=
\frac{-t_{D}}
{\left[\...
...frac{\left(S_r-S_s\right)\tan \gamma}{\cos ^2 \alpha_x}
\right],
&\end{eqnarray}](img81.gif)
![\begin{eqnarray}
&
\frac{\partial L}{\partial \gamma}
=
\frac{-t_{D}}
{\left[\le...
...frac{\left(S_r-S_s\right)\tan \alpha_x}{\cos ^2 \gamma}
\right].
&\end{eqnarray}](img82.gif)