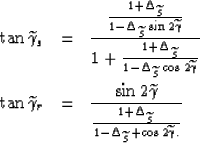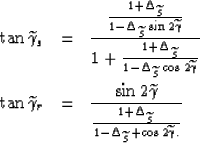Next: Analytical evaluation of the
Up: Biondi: Anisotropic ADCIGs
Previous: REFERENCES
In this appendix I present the expressions for evaluating
the true reflection angles 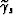 and
and 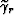 for the incident and reflected plane waves,
from the `normalized slowness difference''
for the incident and reflected plane waves,
from the `normalized slowness difference''
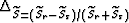 and from the average aperture angles
and from the average aperture angles 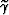 computed by solving equations 16 and 17.
computed by solving equations 16 and 17.
Rosales and Biondi (2005) derived these relationships as follows:
| 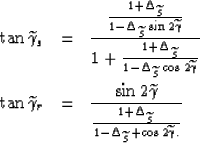 |
(30) |
| (31) |
It is easy to verify that when 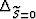 (isotropic case) we get,
as expected,
(isotropic case) we get,
as expected,
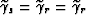 .B
.B





Next: Analytical evaluation of the
Up: Biondi: Anisotropic ADCIGs
Previous: REFERENCES
Stanford Exploration Project
11/1/2005