




Next: About this document ...
Up: Analytical evaluation of the
Previous: Analytical evaluation of the
The application to the isotropic case is simpler
than the anisotropic case because the derivative
of the path length is zero,
but it is instructive since it verifies known results
through a completely different derivation.
Substituting
equations 35 into
equation 33,
I obtain:
| ![\begin{eqnarray}
\left.
\frac{\partial z_\xi}{\partial h_\xi}
\right\vert _{m_\x...
...n ^2\alpha_x\tan ^2 \gamma
\right]
}
\nonumber
\\ &=&
\tan \gamma,\end{eqnarray}](img83.gif) |
|
| |
| (38) |
which shows that 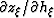 is independent from the dip angle
is independent from the dip angle 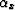 .This expression is consistent with the 2-D analysis
by Sava and Fomel (2003) and
the 3-D analysis by
by Biondi and Tisserant (2004).
.This expression is consistent with the 2-D analysis
by Sava and Fomel (2003) and
the 3-D analysis by
by Biondi and Tisserant (2004).





Next: About this document ...
Up: Analytical evaluation of the
Previous: Analytical evaluation of the
Stanford Exploration Project
11/1/2005
![\begin{eqnarray}
\left.
\frac{\partial z_\xi}{\partial h_\xi}
\right\vert _{m_\x...
...n ^2\alpha_x\tan ^2 \gamma
\right]
}
\nonumber
\\ &=&
\tan \gamma,\end{eqnarray}](img83.gif)
![\begin{eqnarray}
\left.
\frac{\partial z_\xi}{\partial h_\xi}
\right\vert _{m_\x...
...n ^2\alpha_x\tan ^2 \gamma
\right]
}
\nonumber
\\ &=&
\tan \gamma,\end{eqnarray}](img83.gif)