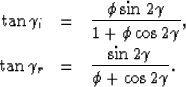Next: Numerical analysis
Up: Kinematic equations
Previous: A Fourier domain look
From equation (3) we established a relation between the
propagation angles for the down-going and up-going plane-waves,
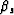 and
and 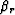 , respectively.
Now, from Figure
, respectively.
Now, from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) it is easy to see that the
propagation angles are related to: 1) the incidence angle of
the down-going plane wave into the reflector (
it is easy to see that the
propagation angles are related to: 1) the incidence angle of
the down-going plane wave into the reflector (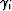 );
2) the reflection angle of the up-going plane wave (
);
2) the reflection angle of the up-going plane wave (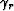 );
and the structural dip (
);
and the structural dip (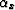 ). The relation among all the angles is
). The relation among all the angles is
| 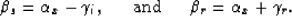 |
(11) |
Combining equation (3) and (11), we can see the
direct relation between the angles that we compute with relations (7)
and/or (10) and the real structural dip, the incidence angle, and
the reflection angle. That is:
| 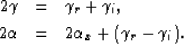 |
|
| (12) |
It is easy to note that the opening angle 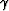 is the reflection angle and
is the reflection angle and  is the
geological dip when
is the
geological dip when
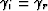 , which is only valid for the single-mode case.
, which is only valid for the single-mode case.
With these equations and Snell's law, we can convert the full-aperture angle (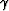 )obtained with equation (7) or (10) into the incidence angle (
)obtained with equation (7) or (10) into the incidence angle (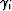 ) or
the reflection angle (
) or
the reflection angle (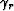 ):
):
| 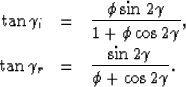 |
|
| (13) |
Appendix A presents a full derivation of the same equations but with the perspective of the
Kirchhoff approach. The reader is encourage to follow that demonstration.





Next: Numerical analysis
Up: Kinematic equations
Previous: A Fourier domain look
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) it is easy to see that the
propagation angles are related to: 1) the incidence angle of
the down-going plane wave into the reflector (
it is easy to see that the
propagation angles are related to: 1) the incidence angle of
the down-going plane wave into the reflector (![]() )obtained with equation (7) or (10) into the incidence angle (
)obtained with equation (7) or (10) into the incidence angle (![]() ) or
the reflection angle (
) or
the reflection angle (![]() ):
):