




Next: Transformation into independent angles
Up: Kinematic equations
Previous: Kinematic equations
It is also possible to implement the transformation to full-aperture angle in the Fourier domain.
Although this transformation does not take into account the lateral and vertical
variations of 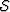 , it's still an interesting exercise.
We can link this theory with Fourier transform by knowing that:
, it's still an interesting exercise.
We can link this theory with Fourier transform by knowing that:
| 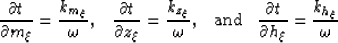 |
(8) |
From equations (8), it is well known that
| 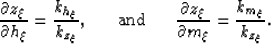 |
(9) |
Therefore, the Fourier equivalent for equations (7) is
| ![\begin{eqnarray}
-\tan{\gamma} &=& \frac{\mathcal{S}^2 -1 \pm
\sqrt{ (1-\mathca...
...} \mathcal{S}-
\frac{k_{m_\xi}}{k_{z_\xi}} \mathcal{S}^2 \right]}.\end{eqnarray}](img26.gif) |
|
| (10) |
Equations (10) can be used to transform SODCIGs into full-aperture ADCIGs
through stretching of the offset and midpoint axes, but this is only valid for a
velocity-ratio function 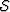 that is constant along the image (
that is constant along the image (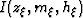 ).
).





Next: Transformation into independent angles
Up: Kinematic equations
Previous: Kinematic equations
Stanford Exploration Project
5/3/2005
![\begin{eqnarray}
-\tan{\gamma} &=& \frac{\mathcal{S}^2 -1 \pm
\sqrt{ (1-\mathca...
...} \mathcal{S}-
\frac{k_{m_\xi}}{k_{z_\xi}} \mathcal{S}^2 \right]}.\end{eqnarray}](img26.gif)