Next: Discussion and Future Work
Up: Shragge and Sava: Migration
Previous: Riemannian Wavefield Extrapolation
We test the combined conformal mapping and Riemannian wavefield
extrapolation approach on a synthetic dataset computed on a rugged
topographic surface. The geological model is a merger of common
geologic features from the Canadian
Foothills in northeastern British Columbia, Canada.
The velocity model, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , consists
of steep thrust fault planes and complex folds typical of
a mountainous thrust region. The topographic boundary of interest
is demarcated by the velocity model discontinuity nearest to the
surface. The total relief of the Earth's surface in this model is
approximately 1600 m. Also note that the complex near-surface velocity
structure should present a significant imaging challenge Gray and Marfurt (1995).
Foothills.vel
, consists
of steep thrust fault planes and complex folds typical of
a mountainous thrust region. The topographic boundary of interest
is demarcated by the velocity model discontinuity nearest to the
surface. The total relief of the Earth's surface in this model is
approximately 1600 m. Also note that the complex near-surface velocity
structure should present a significant imaging challenge Gray and Marfurt (1995).
Foothills.vel
Figure 5 Foothills velocity model
constructed from composite 2-D geologic model from northeastern
British Columbia, Canada. Total elevation relief is approximately
1600 m. The topographic boundary of interest is demarcated by the
velocity model discontinuity nearest to the surface.





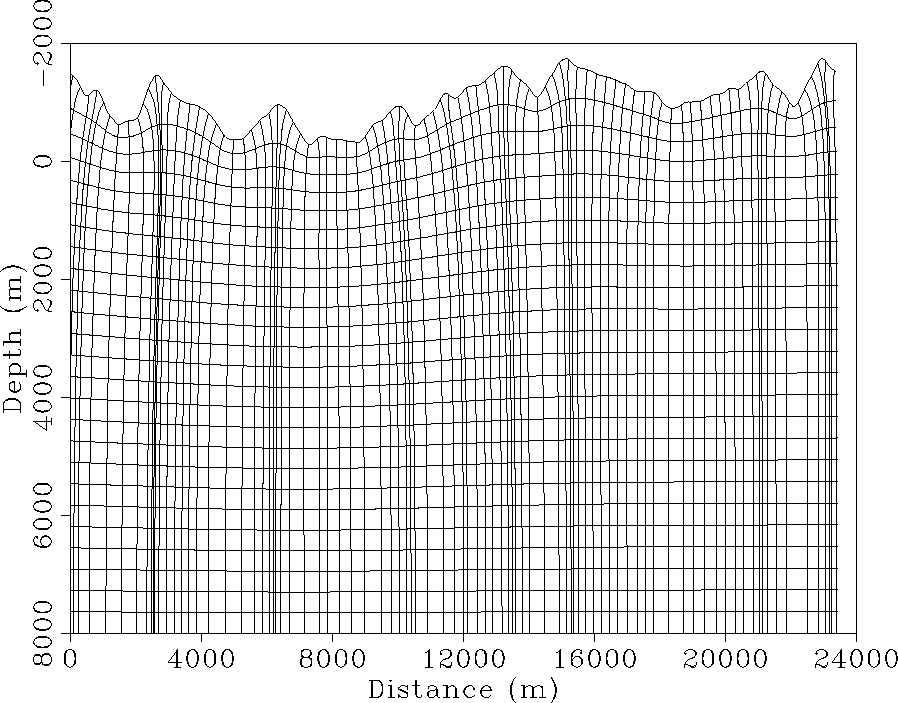
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of using conformal
mapping to construct a coordinate system that incorporates the
topography shown in Figure
shows the result of using conformal
mapping to construct a coordinate system that incorporates the
topography shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . One important
observation is that topography causes focusing of the coordinate
system. In particular, the coordinate system compresses under local
topographic maxima, and expands beneath local topographic minima.
This suggests that Jacobian spreading factor, J, in
(3) will be strongly dependent on the local
radius of curvature of the topographic surface. However, as the
topographic fronts move farther from the surface, the topographic
influenced diminishes and the fronts move toward becoming a flat
datum. (Hence, this approach could be used for wavefield datuming.)
. One important
observation is that topography causes focusing of the coordinate
system. In particular, the coordinate system compresses under local
topographic maxima, and expands beneath local topographic minima.
This suggests that Jacobian spreading factor, J, in
(3) will be strongly dependent on the local
radius of curvature of the topographic surface. However, as the
topographic fronts move farther from the surface, the topographic
influenced diminishes and the fronts move toward becoming a flat
datum. (Hence, this approach could be used for wavefield datuming.)
Foothills.coords
Figure 6 Topographic coordinate
system constructed using conformal mapping. Note the
compression of the rays under topographic maxima, and their
extension under topographic minima. The influence of topography on
the coordinate system diminishes farther from the surface.





A prestack wave-equation imaging test was conducted using a synthetic
data set generated by an acoustic, 2-D, finite-difference code through
the model shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The data set
is comprised of 278 shot gathers with a split-spread geophone geometry
where absolute offsets range between 15 m and 3600 m. Geophone and
source spacing are 15 m and 90 m, respectively. Data were generated
on a regular Cartesian mesh. Thus, we interpolated the data to fit on
a grid uniform along the topographic surface. Data fidelity may have
been lowered by this processing step; however, we emphasize that this
step is normally of modest importance since field data likely are
nearly uniformly-spaced on the topographic surface.
. The data set
is comprised of 278 shot gathers with a split-spread geophone geometry
where absolute offsets range between 15 m and 3600 m. Geophone and
source spacing are 15 m and 90 m, respectively. Data were generated
on a regular Cartesian mesh. Thus, we interpolated the data to fit on
a grid uniform along the topographic surface. Data fidelity may have
been lowered by this processing step; however, we emphasize that this
step is normally of modest importance since field data likely are
nearly uniformly-spaced on the topographic surface.
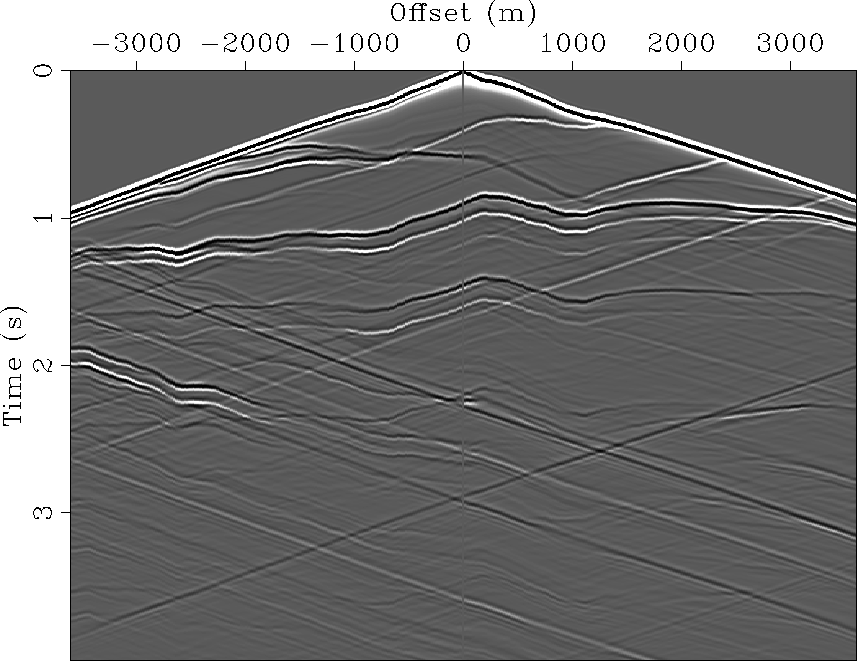
A sample shot record at horizontal location 14040 m is shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Note that the relief causes
non-linear moveout of the direct arrival, and a substantial amount of
topographic scattering as illustrated by the horizontal banding across
the section. No preprocessing of the sections was done to remove
these two potential noise sources, and the resulting image is
contaminated accordingly.
. Note that the relief causes
non-linear moveout of the direct arrival, and a substantial amount of
topographic scattering as illustrated by the horizontal banding across
the section. No preprocessing of the sections was done to remove
these two potential noise sources, and the resulting image is
contaminated accordingly.
singleshot
Figure 7 Shot record from source
station 14040 m that shows the influence of topography.
Note the non-linear moveout of the direct arrivals, and the
significant amount of topographic scattering typified by horizontal
streaking across the section.
|
|  |





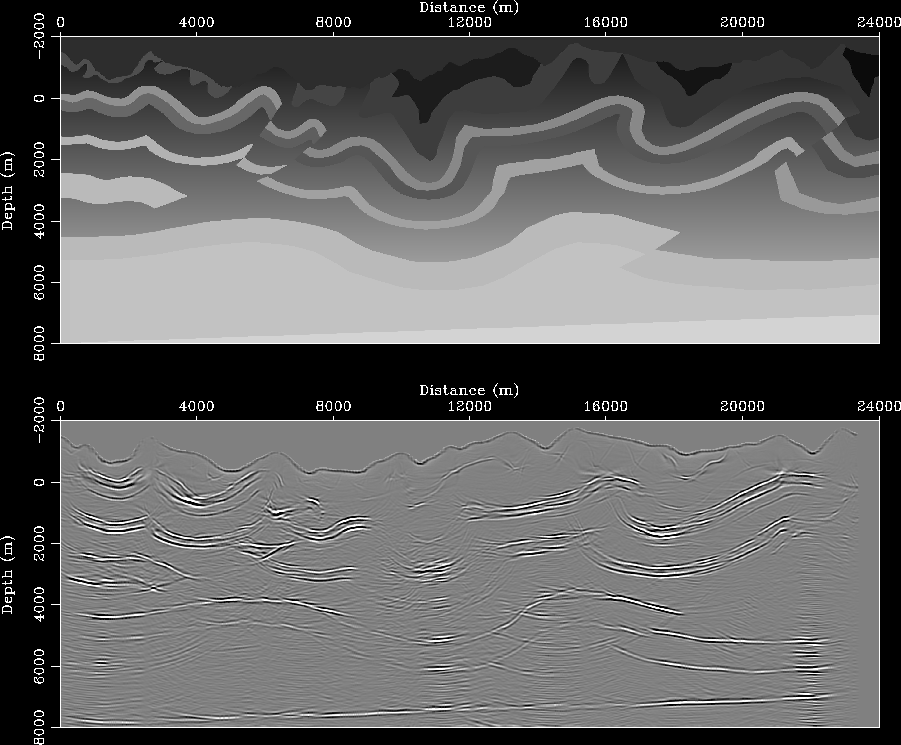
A preliminary prestack migration image is presented in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The majority of reflectors are
well positioned; however, diffractions and discontinuous
reflectors exist at locations directly beneath topographic minima and
maxima. Although these anomalies may be caused by the data
regularization procedure, they more likely arise from limitations
imposed by the phase-screen approximation.
. The majority of reflectors are
well positioned; however, diffractions and discontinuous
reflectors exist at locations directly beneath topographic minima and
maxima. Although these anomalies may be caused by the data
regularization procedure, they more likely arise from limitations
imposed by the phase-screen approximation.
Also present are vertical streaks of higher (lower) amplitude
directly under local topographic minima (maxima). We attribute these
anomalous amplitudes to a combination of: i) the simplicity of the
weighing function used in the interpolation of the image between the
topographic and Cartesian coordinate systems; and ii) our
non-consideration of the dynamic terms in
(6). Geological structure poorly imaged or
absent include sections of the steeply-dipping fold
belt, which is probably due to limitations imposed by both the limited
angular bandwidth of the phase-screen approximation, and our use of
only one reference medium.
prestackimage
Figure 8 Top: Foothills thrust model
velocity model. Bottom: The preliminary prestack migration image using
Riemannian wavefield extrapolation on a coordinate system generated
through conformal mapping.










Next: Discussion and Future Work
Up: Shragge and Sava: Migration
Previous: Riemannian Wavefield Extrapolation
Stanford Exploration Project
10/23/2004

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , consists
of steep thrust fault planes and complex folds typical of
a mountainous thrust region. The topographic boundary of interest
is demarcated by the velocity model discontinuity nearest to the
surface. The total relief of the Earth's surface in this model is
approximately 1600 m. Also note that the complex near-surface velocity
structure should present a significant imaging challenge Gray and Marfurt (1995).
, consists
of steep thrust fault planes and complex folds typical of
a mountainous thrust region. The topographic boundary of interest
is demarcated by the velocity model discontinuity nearest to the
surface. The total relief of the Earth's surface in this model is
approximately 1600 m. Also note that the complex near-surface velocity
structure should present a significant imaging challenge Gray and Marfurt (1995).