




Next: Conclusions
Up: Shragge and Sava: Migration
Previous: Numerical examples
The issues below are important for improving the quality of
wave-equation migration directly from topography images. In some
cases, we discuss ideas not yet implemented, while in others we
speculate on directions of future research.
- Muting direct arrivals:
- We did not mute out the direct
arrivals from the shot gathers, which probably introduced
artifacts. In principle, a first-arrival mute is fairly easy to
implement; however, their non-linear moveout requires introducing
more complicated muting functions. In the future, we will eliminate
this source of image contamination.
- Using improved mapping weighting functions:
- We speculate that
amplitudes could become more uniform along the reflectors through the
use of a better weighting function. The image is currently
interpolated to the Cartesian domain using sinc-function operators,
where the image points are weighted by the mapping fold. A better
weighting function should include the Jacobian of the transformation
between the two coordinate systems.
- Including dynamic propagation terms:
- We have incorporated only
the second-order partial differential terms in the phase-screen approximation for
extrapolation direction wavenumber,
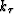 . Including the remaining
two dynamic terms should lead to reflectors of more uniform
intensity, since these terms contribute to wavefield amplitudes.
. Including the remaining
two dynamic terms should lead to reflectors of more uniform
intensity, since these terms contribute to wavefield amplitudes.
- Incorporating multiple reference media:
- The above image was
generated using one reference medium (i.e., we performed Taylor
expansions about a0 and b0). However, in practice many
reference media (e.g., velocities) are often used to generate images
through the PSPI approach. Noting that the variability of
coordinate spacing is significant (and functions a and b
thereby), we surmise that the incorporation of multiple reference
media is likely necessary to eliminate existing kinematic errors and
to improve diffraction focusing.
- Implementing a seperate wavefield datuming step:
- By extension,
we have shown that this procedure works as a datuming
procedure. For example, a coordinate system generated by conformal
mapping could be used in an upward continuation scheme to establish
the wavefield at a uniform level above topography. Standard
Cartesian migration technology could then be applied directly to
migrate the datumed wavefield.





Next: Conclusions
Up: Shragge and Sava: Migration
Previous: Numerical examples
Stanford Exploration Project
10/23/2004