




Next: Numerical examples
Up: Shragge and Sava: Migration
Previous: Conformal Mapping
Performing wavefield extrapolation on topographic computational meshes
computed through conformal mapping requires parameterizing the
acoustic wave-equation by a set of variables that describe the
coordinate system. In 2-D, we denote these variables the
extrapolation direction,  , (analogous to depth in Cartesian wavefield
extrapolation), and the direction orthogonal,
, (analogous to depth in Cartesian wavefield
extrapolation), and the direction orthogonal, 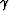 (analogous to
horizontal offset in Cartesian wavefield extrapolation). Variables
(analogous to
horizontal offset in Cartesian wavefield extrapolation). Variables
 and
and 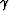 are related to the topographic coordinate system point
set through
are related to the topographic coordinate system point
set through 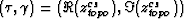 .Figure
.Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents a sketch of the topographic
coordinate system geometry.
presents a sketch of the topographic
coordinate system geometry.
topocoord
Figure 4 Cartoon illustrating the topography
coordinate system. Variable 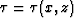 is the extrapolation
direction and parameter is the extrapolation
direction and parameter 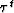 may be considered a topographic
``front''. Variable may be considered a topographic
``front''. Variable 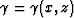 is the coordinate across the
extrapolation step at a constant is the coordinate across the
extrapolation step at a constant  step, and parameter step, and parameter 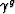 may
be considered a topographic ``ray''. may
be considered a topographic ``ray''.
|
| 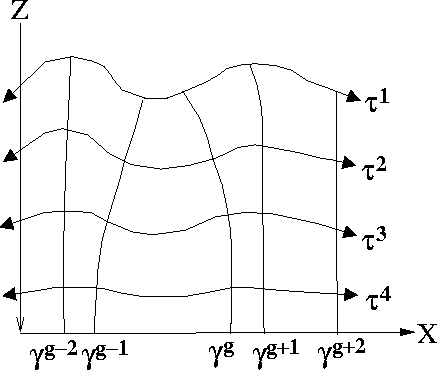 |

The 2-D acoustic wave-equation for wavefield, 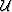 , at frequency,
, at frequency,
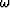 , governing propagation in topographic coordinates is
Sava and Fomel (2004),
, governing propagation in topographic coordinates is
Sava and Fomel (2004),
| ![\begin{displaymath}
\frac{1}{\alpha J} \left[ \frac{\partial}{\partial\t} \left(...
... U}}{\partial\gamma} \right) \right]=
-\omega^2 s^2 {\cal U}, \end{displaymath}](img28.gif) |
(3) |
where s is the slowness of the medium,  a distance
scaling factor in the extrapolation direction
a distance
scaling factor in the extrapolation direction  , and J a
Jacobian of transformation of coordinate
, and J a
Jacobian of transformation of coordinate 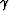 (analogous to a
geometrical ray spreading factor). Parameters
(analogous to a
geometrical ray spreading factor). Parameters  and J are
defined by,
and J are
defined by,
| ![\begin{eqnarray}
\alpha=& \left[ \frac{\partial x}{\partial\t} \frac{\partial x}...
...\frac{\partial z}{\partial\gamma} \right]^{\frac{1}{2}}, \nonumber\end{eqnarray}](img30.gif) |
(4) |
| |
where x and z are the coordinates of the underlying Cartesian
basis. Note that parameters  and J are solely components
of the coordinate system and are independent of the extrapolated
wavefield values.
and J are solely components
of the coordinate system and are independent of the extrapolated
wavefield values.
Analogous to wavefield continuation on a Cartesian mesh, a dispersion
relation must be specified that forms the basis for all derived
extrapolation operators in a topographic coordinate system. The
relation being sought is the wavenumber along the extrapolation
direction, 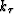 . Following Sava and Fomel (2004), the partial
derivative operators in (3) are expanded out to
generate a second-order partial differential equation with non-zero
cross derivatives. Fourier-domain wavenumbers are then substituted
for the partial differential operators acting on wavefield,
. Following Sava and Fomel (2004), the partial
derivative operators in (3) are expanded out to
generate a second-order partial differential equation with non-zero
cross derivatives. Fourier-domain wavenumbers are then substituted
for the partial differential operators acting on wavefield, 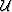 , and
the quadratic formula is applied to yield the expression for
, and
the quadratic formula is applied to yield the expression for 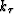 ,
,
| ![\begin{displaymath}
k_\tau= \frac{{\rm i}\alpha}{2 J} \frac{\partial}{\partial \...
...amma- \frac{\alpha^2}{J^2} k_\gamma^2
\right]^{\frac{1}{2}}. \end{displaymath}](img32.gif) |
(5) |
One relatively straightforward way to apply wavenumber 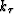 in an
extrapolation scheme is to develop the topographic coordinate system
equivalent to a phase-screen extrapolation operator
Sava (2004). In the following example, we treat solely
the kinematic, one-way propagation of recorded wavefields. This
asymptotic approximation leads us to drop the first order partial
differential terms in (5),
in an
extrapolation scheme is to develop the topographic coordinate system
equivalent to a phase-screen extrapolation operator
Sava (2004). In the following example, we treat solely
the kinematic, one-way propagation of recorded wavefields. This
asymptotic approximation leads us to drop the first order partial
differential terms in (5),
| 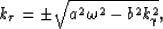 |
(6) |
where 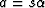 and
and 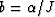 . The expansion of
. The expansion of 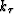 about
reference parameters a0 and b0 is,
about
reference parameters a0 and b0 is,
| 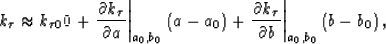 |
(7) |
where subscript denotes reference. Partial derivatives with
respect to parameters a and b are,
| 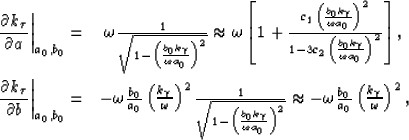 |
(8) |
| |
where the square root function in the denominator has been expanded
using a Padé approximation. The choice of numerical constants
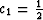 and c2=0 yields a 15 finite-difference
term. Thus, the phase-screen approximation for extrapolation
wavenumber,
and c2=0 yields a 15 finite-difference
term. Thus, the phase-screen approximation for extrapolation
wavenumber, 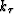 , is,
, is,
| 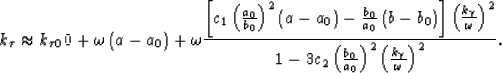 |
(9) |
This expression can be generalized to include multiple reference media
through a phase-shift plus interpolation (PSPI) approach
Gazdag and Sguazzero (1984) over the two parameters; however, this extension is
not treated here. The approximation for wavenumber, 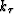 , given in
(9) is used in a conventional wavefield
extrapolation scheme that extends the recorded wavefield away from the
acquisition surface to the required subsurface locations. This
involves solving a one-way wave-equation which, in discrete
extrapolation steps of
, given in
(9) is used in a conventional wavefield
extrapolation scheme that extends the recorded wavefield away from the
acquisition surface to the required subsurface locations. This
involves solving a one-way wave-equation which, in discrete
extrapolation steps of 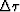 , requires a recursive computation
of the following:
, requires a recursive computation
of the following:
| 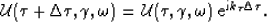 |
(10) |
Our prestack migration example is computed using a shot
profile migration code. This involves extrapolating the source and
receiver wavefields, 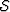 and
and 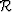 , independently using,
, independently using,
| 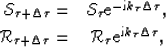 |
(11) |
| |
and applying an imaging condition at each extrapolation level to
generate image, 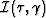 ,
,
| 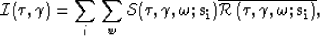 |
(12) |
where the line over the receiver wavefield indicates complex
conjugate. Image 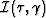 is then mapped to a Cartesian
coordinate system using sinc-based interpolation operators in the
neighborhood of each mapped point to generate the final image,
is then mapped to a Cartesian
coordinate system using sinc-based interpolation operators in the
neighborhood of each mapped point to generate the final image,
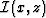 .
.





Next: Numerical examples
Up: Shragge and Sava: Migration
Previous: Conformal Mapping
Stanford Exploration Project
10/23/2004
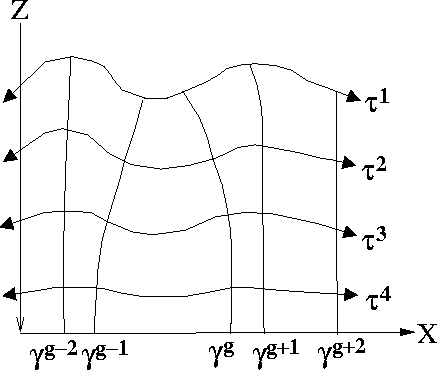
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents a sketch of the topographic
coordinate system geometry.
presents a sketch of the topographic
coordinate system geometry.
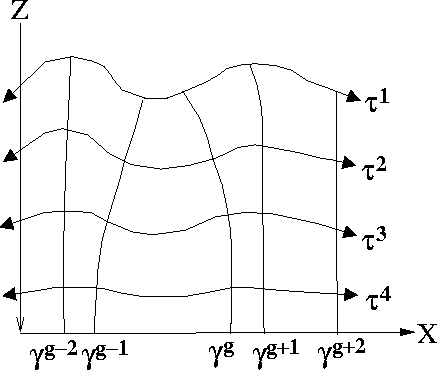
![]() , at frequency,
, at frequency,
![]() , governing propagation in topographic coordinates is
Sava and Fomel (2004),
, governing propagation in topographic coordinates is
Sava and Fomel (2004),
![\begin{eqnarray}
\alpha=& \left[ \frac{\partial x}{\partial\t} \frac{\partial x}...
...\frac{\partial z}{\partial\gamma} \right]^{\frac{1}{2}}, \nonumber\end{eqnarray}](img30.gif)
![]() . Following Sava and Fomel (2004), the partial
derivative operators in (3) are expanded out to
generate a second-order partial differential equation with non-zero
cross derivatives. Fourier-domain wavenumbers are then substituted
for the partial differential operators acting on wavefield,
. Following Sava and Fomel (2004), the partial
derivative operators in (3) are expanded out to
generate a second-order partial differential equation with non-zero
cross derivatives. Fourier-domain wavenumbers are then substituted
for the partial differential operators acting on wavefield, ![]() , and
the quadratic formula is applied to yield the expression for
, and
the quadratic formula is applied to yield the expression for ![]() ,
,
![\begin{displaymath}
k_\tau= \frac{{\rm i}\alpha}{2 J} \frac{\partial}{\partial \...
...amma- \frac{\alpha^2}{J^2} k_\gamma^2
\right]^{\frac{1}{2}}. \end{displaymath}](img32.gif)
![]() in an
extrapolation scheme is to develop the topographic coordinate system
equivalent to a phase-screen extrapolation operator
Sava (2004). In the following example, we treat solely
the kinematic, one-way propagation of recorded wavefields. This
asymptotic approximation leads us to drop the first order partial
differential terms in (5),
in an
extrapolation scheme is to develop the topographic coordinate system
equivalent to a phase-screen extrapolation operator
Sava (2004). In the following example, we treat solely
the kinematic, one-way propagation of recorded wavefields. This
asymptotic approximation leads us to drop the first order partial
differential terms in (5),
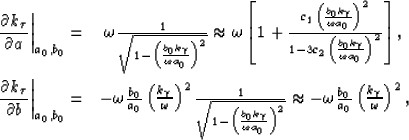
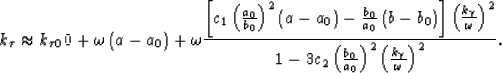
![]() and
and ![]() , independently using,
, independently using,