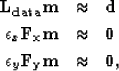Next: Example
Up: Curry: Midpoint-offset vs. source-receiver
Previous: INTRODUCTION
Prediction-error filter (PEF) based interpolation can be cast as a two
stage linear least-squares process Claerbout (1999), where a PEF is first estimated on the known data.
Then, the output of
convolution of the newly-found PEF with the desired model is minimized while
fixing the known data. The first stage of the process can be
described mathematically by
| 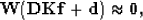 |
(1) |
where the known data (d) is convolved (D) with a PEF with
unknown coefficients (f), except for the first, which is
constrained by K to be 1. If there are areas where the filter
is being convolved with unknown data, those areas are weighted to
by a diagonal weight W.
The second stage can be described by
| 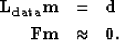 |
|
| (2) |
In the second fitting goal, L is
a selector matrix that is 1 where there is a data point and
where there isn't, m is the interpolated output, d is once
again the known data, and F represents convolution with the
newly-found PEF.
In the case of a non-stationary PEF, where the filter varies with
position, a second fitting goal has to be added to the first stage of
the interpolation process, so that the now much greater number of
filter coefficients becomes adequately constrained. This fitting goal
can be expressed as
| 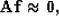 |
(3) |
where A is a regularization operator (typically a Laplacian)
that operates spatially over each filter coefficient separately, and
f is the non-stationary PEF. Fitting goal (1) is
written identically for the non-stationary case, but each of the
operators present (as well as the filter) are now non-stationary. A
full description of what the matrices for non-stationary PEFs look
like is given in SEP-113 Guitton (2003).
Typically, when interpolating data that are regularly-sampled, the
filter is interlaced so that the filter skips over the missing traces,
which allows a filter to be estimated Crawley (2000). Once the filter has been
estimated, the interlacing of the filter is undone for the second stage of the
interpolation process.
When the data are not regularly-sampled, the interlacing approach
usually fails. In this case, a multi-scale approach can be used where
a non-stationary PEF can be estimated on multiple regridded copies of
the original data
Curry and Brown (2001); Curry (2002, 2003).
This can be expressed as
| ![\begin{displaymath}
\bf W \left( \left[ \begin{array}
{c}
\bf D_0 \\
\bf D_...
...... \\
\bf d_n \\
\end{array} \right] \right) \approx 0
.\end{displaymath}](img4.gif) |
(4) |
Here, the different scales of data 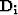 are generated by
the normalized adjoint of linear interpolation, which takes points from a
fine grid and sprays them into the coarser grid, then normalizes by
the fold. The weight W is now a diagonal weight for all scales
of data, while the introduction of a sub-sampling operator P
subsamples the non-stationary filter so that the spatial size of the
filter will match the size of the rescaled data.
are generated by
the normalized adjoint of linear interpolation, which takes points from a
fine grid and sprays them into the coarser grid, then normalizes by
the fold. The weight W is now a diagonal weight for all scales
of data, while the introduction of a sub-sampling operator P
subsamples the non-stationary filter so that the spatial size of the
filter will match the size of the rescaled data.
Another possible approach is to use a pair of non-stationary
2D PEFs which are estimated independently from the original unscaled
data using fitting goals (1) and (3) in
two different directions. Once
these two PEFs have been estimated, they could be used in tandem to
interpolate missing data by Claerbout (1999); Curry (2004):
| 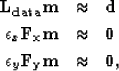 |
|
| |
| (5) |
where 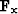 and
and 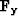 are 2D non-stationary PEFs (compared
to the typically-3D PEF shown before in fitting goal
2),
are 2D non-stationary PEFs (compared
to the typically-3D PEF shown before in fitting goal
2), 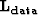 selects known data points, d is
still the known data and m the unknown model. Unlike the
multi-scale approach, this method requires that the data are
evenly-sampled along tracks oriented in two different directions.
selects known data points, d is
still the known data and m the unknown model. Unlike the
multi-scale approach, this method requires that the data are
evenly-sampled along tracks oriented in two different directions.





Next: Example
Up: Curry: Midpoint-offset vs. source-receiver
Previous: INTRODUCTION
Stanford Exploration Project
10/23/2004
![\begin{displaymath}
\bf W \left( \left[ \begin{array}
{c}
\bf D_0 \\
\bf D_...
...... \\
\bf d_n \\
\end{array} \right] \right) \approx 0
.\end{displaymath}](img4.gif)