Electric field of the metal hammer plate

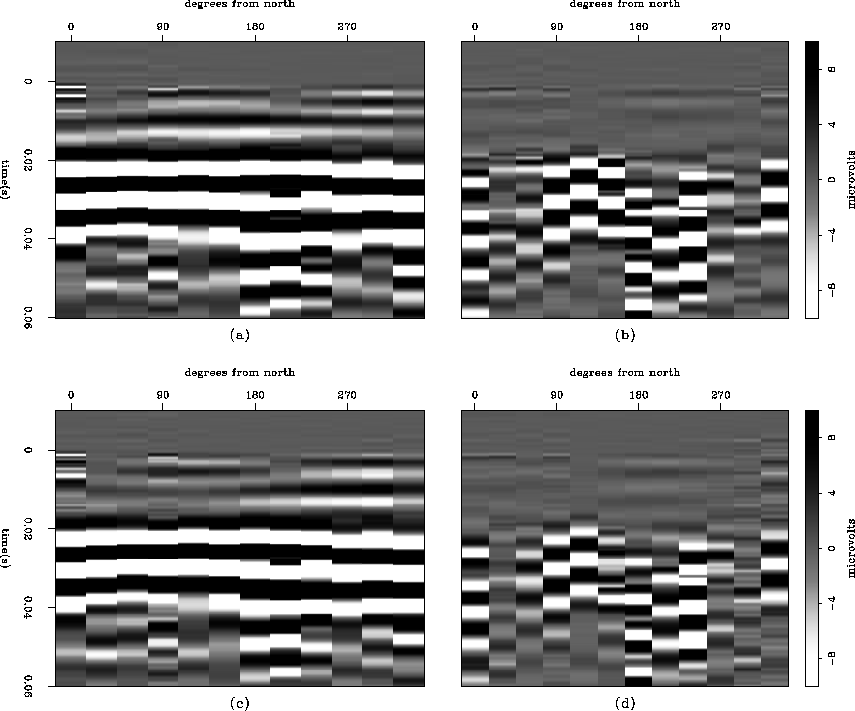
One important observation about the Lorentz field is that its polarity reverses between sequential hammer strikes, such that approximately half of the raw hammer gathers show one polarity, and the other half show the opposite polarity. The stacks shown in Figures 2d and 3c are made from shot gathers selected on the basis of the polarity of the Lorentz field. The other gathers would produce a stack with a Lorentz field arrival with opposite polarity. A stack of all of the shot gathers would show very little Lorentz energy as it tends to stack out.

Data collected by the circular electrode array using the sledgehammer on the aluminum hammer plate are shown in Figure 6. Figure 6a and b are the radial and tangential parts of a partial stack of hammer strikes, and 6c and d are the radial and tangential parts of a stack of the other hammer strikes. These two sets of impacts were selected from the individual hammer strike gathers based on the presence and polarity of the events that appear at a time of $\sim$0.001 seconds at certain radial positions (90-180 and 240-330) in the radial component and 90 out of phase (0-90 and 180-270) in the tangential component. Note that the polarity of these arrivals is reversed between the two stacks (Figure 6a and b, versus Figure 6c and d).

 

circle2
Figure 6 Electroseismic data collected with a sledgehammer on the aluminum hammer plate and recorded by the circular electrode array. Lorentz energy can be seen at $\sim$0.001 s in each gather. a) Radial component of stack of selected hammer strikes. Note Lorentz energy at $\sim$0.001 s at certain radial positions. b) Tangential component of the same stacked gathers, with faint Lorentz energy at $\sim$0.001 s at positions orthogonal to the energy in a). c) Radial component of a stack of other shot gathers, with similar energy at $\sim$0.001 s but with reversed polarity relative to a). d) Tangential component of stack of the same gathers as c), again showing Lorentz energy at positions orthogonal to the energy in c).

The radial pattern of these arrivals suggests that they are due to a horizontal electric dipole oriented a few tens of degrees west of north, with the orientation of the dipole reversed between the two sets of gathers. Because the field occurs only for hammer impacts on a metal plate, we assume that it is caused by the metal plate, and that it is the Lorentz field (Equation 3). Because the orientation of the dipole reverses phase between sequential hammer impacts, we must assume that it is caused by a component of ${\bf v} \times{\bf B}$ that can reverse from one strike to the next. The earth's magnetic field ${\bf B}$ is essentially constant (oriented toward magnetic north, and inclined at an angle of $\sim$60 from horizontal), so we must look to ${\bf v}$ for this reversal. Although the dominant component of ${\bf v}$ is vertical, there is also a small horizontal component due to the imperfect impact of the hammer on the rounded top of the aluminum block. For the case of the in-line data (Figure 2d and Figure 3c), the aluminum cylinder is oriented along the electrode receiver line, and thus the hammer strikes will tend to cause horizontal motion perpendicular to the line. If we take the cross product of this velocity with the vertical component of ${\bf B}$, we get a horizontal electric field ${\bf E}$ oriented along the electrode line, just as we observe. The orientation of the horizontal component of ${\bf v}$ will vary from strike to strike, but will generally be perpendicular to the electrode transect line, in one of two primary polarities. We conclude that the observed electric field is due to the horizontal component of the hammer plate velocity crossed with the vertical component of the earth's magnetic field.

 

circ_amps Figure 7 Comparison between real and modeled Lorentz energy as a function of radial position. a) Amplitude (solid=radial, dashed=tangential) patterns extracted from the stacks in Figure 6a and b. b) Amplitudes extracted from stacks in Figure 6c and d. c) Amplitude pattern modeled for a dipole oriented 50 west of north.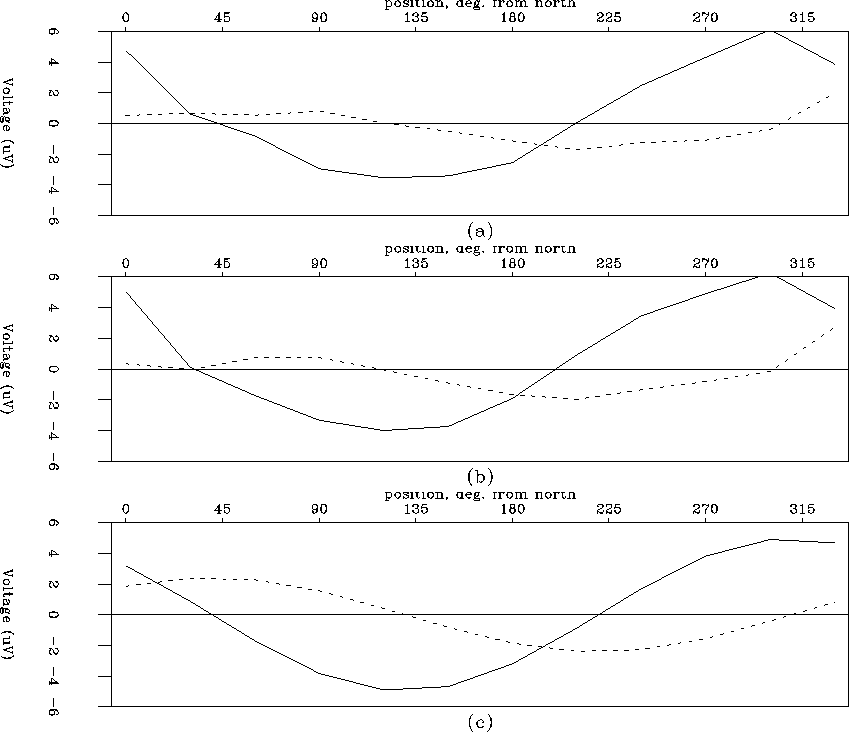

Next we extract the amplitudes of the observed arrivals and compare them with modeled amplitudes. Figure 7a shows the amplitude of the Lorentz field event shown in Figure 6a and b, while Figure 7b shows the amplitude of the Lorentz in Figure 6c and d. The radial component is plotted as a solid line and the tangential component as a dashed line. The amplitude in Figure 7a corresponds with the third of the three phases of the Lorentz field arrival in Figure 6a (0.0042 to 0.0065 seconds) while the amplitude in Figure 7b was extracted from the second of the three main phases of the Lorentz event in Figure 6b (0.0025 to 0.0045 seconds), thus the two amplitude patterns are in-phase while the two displayed Lorentz events are 180 out-of-phase. We use Equation (4) to model a horizontal dipole at the source point, and find that a best fit is achieved with a dipole oriented $\sim$50 west of north. This alignment corresponds with the alignment of the hammer plate and the person swinging the hammer, not with magnetic north, confirming our interpretation that the horizontal ${\bf v}$ of the hammer plate and the vertical component of the earth's field ${\bf B}$ are responsible for the Lorentz field. The horizontal component of ${\bf B}$ does not seem to play a role in the creation of this field.

 

metal_amps
Figure 8 In-line data showing the Lorentz field at $\sim$0.001 s, the direct field at $\sim$0.005 s, and modeled and real amplitudes. a) Stacked data shown in Figure 2d, but with lower-frequency bandpass filter (20 to 800 Hz). b) Real amplitudes (dots) of Lorentz field arrival of data in a), and modeled amplitudes (solid line) corresponding with the metal hammer plate acting as an electric dipole oriented along the electrode array. c) Stack of other selected shot gathers (those with Lorentz field arrival opposite in polarity to stack in part a). d) Real (dots) and modeled (solid line) amplitudes for metal plate as a horizontal dipole as predicted by the Lorentz equation.

We can gain further knowledge about the Lorentz field by extracting amplitudes from the in-line data (Figure 2d). Figure 8a and c show stacks of two different sets of impacts collected with the metal hammer plate processed with a broad bandpass filter (20 to 800 Hz); the data in Figure 8a is the same stack as in Figure 2d. Both of these data plots show a strong flat arrival at about 0.002 seconds which we interpret as the Lorentz field, followed by another flat event with reversed polarity on opposite sides of the shot point. This second arrival is the direct field. Amplitudes extracted from these stacks for the Lorentz field are show in Figure 8b and d as dots. Modeled amplitudes for a horizontal electric dipole matching the hammer plate (charge separation of 0.2m between ends of the dipole, lateral offset of 0.25m from the receiver line) are plotted as solid lines. Only the magnitude and polarity of the modeled dipole is varied between the two plots. The central two traces show polarity opposite that of the rest of the Lorentz field because they are located along the horizontal dipole and so are measuring the field off of its main axis, where the field is opposite to the direction of the dipole.