Electroseismic direct field

In order to characterize both the direct field and the Lorentz field, we conducted a series of experiments involving the recording of various sources with electrode pairs deployed in a circular geometry. The electrode array was spaced evenly around a circle of radius 4.3m in a homogeneous part of the vineyard meadow, with 12 electrode pairs oriented radially and 12 oriented tangentially. Thus tangential and radial pairs of electrodes were co-located at 30 degree intervals around the circle. 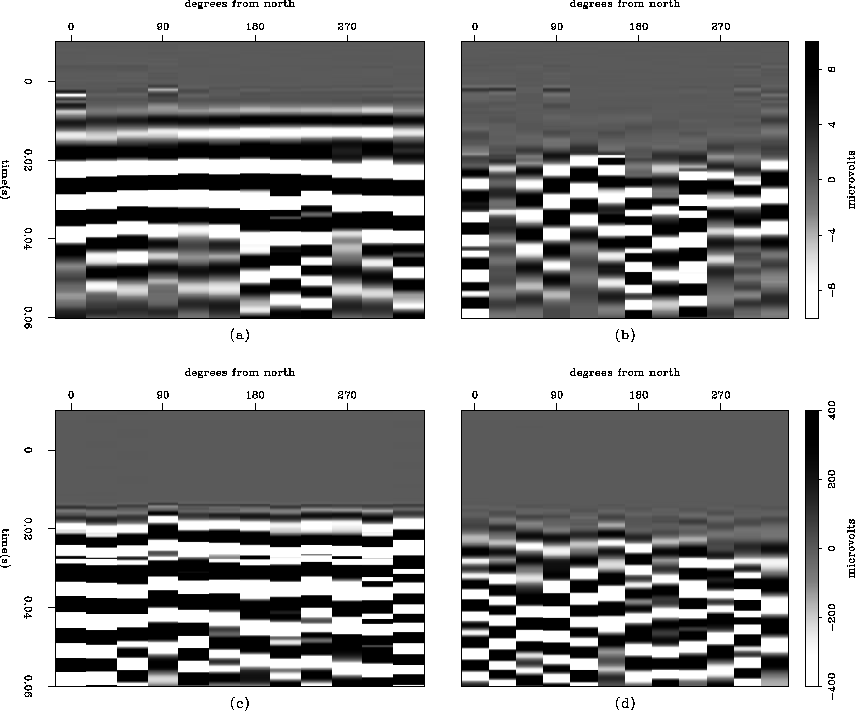The source point is in the center of the circle for all shot gathers. Figure 4a shows the radial traces of a shot gather collected with a sledgehammer striking the plastic plate. Based on arrival times from the data shown in Figure 2, we can interpret the strong coherent arrival at 0.02 seconds as the coseismic energy, and the weaker arrival at 0.01 seconds as the direct field. These arrivals do not appear in the tangential part of the same shot gather (Figure 4b), as is to be expected for a vertical dipole (the direct field) and radially propagating seismic energy (the coseismic arrival). Further confirmation of our interpretation of the 0.02 second arrival as coseismic energy is provided by the corresponding radial horizontal geophone data shown in Figure 4c, where we see that the first seismic arrival closely matches the interpreted coseismic arrival in Figure 4b. The lack of any energy at $\sim$0.01 seconds in Figure 4c supports our interpretation of the 0.01 second energy in Figure 4a as the direct field, or at least as an electroseismic arrival. As is to be expected, the tangential geophone data (Figure 4d) do not show coherent arrivals.

 

circle1
Figure 4 Stacked shot gathers recorded by the circular electrode array described in the text. a) Radial component of electric field created by the impact of a sledgehammer on a plastic hammer plate. Note coherent direct field arrival at $\sim$0.01 sec and coseismic arrival at $\sim$0.02 sec. b) Tangential component of the same shot gather (hammer on plastic plate) with no coherent arrivals. c) Radial component of horizontal geophone data, with first seismic arrival at $\sim$0.02 sec, corresponding with coseismic arrival in a). d) Tangential component of geophone data, with no clear coherent arrivals.

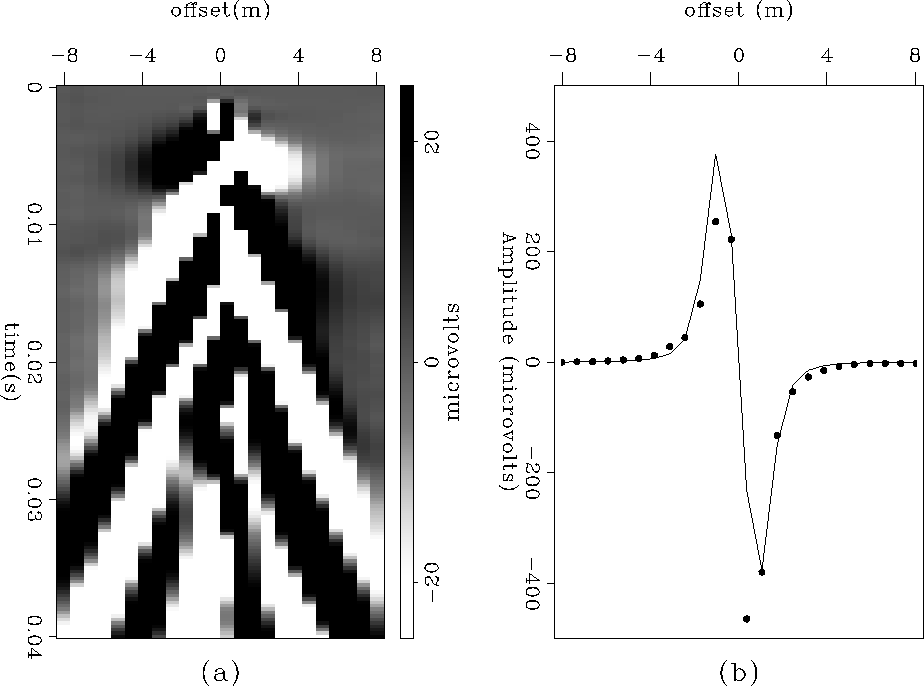
The fact that the direct field energy in Figure 4a shows (approximately) constant amplitudes around the circle is consistent with the interpretation that this energy is due to a vertical dipole. The deviations from constant amplitude are likely caused by imperfect electrode coupling. We can constrain the size and location of this dipole by considering the amplitude pattern of the in-line shot record shown in Figure 2c. Figure 5a shows the same data, but with a lower-frequency bandpass filter (so as to better represent the full direct field, which can be clearly seen as a single strong arrival at $\sim$0.005 seconds). The amplitude of the maximum of this arrival is plotted as dots in Figure 5b. Using the equation for the amplitude pattern of a dipole

 

$$V(x,z) = \frac{qd}{4\pi\epsilon_0} \, \frac{z}{(x^2+y^2)^{3/2}},$$ (4)

(where q is the charge and d is the separation between poles) we model amplitudes corresponding with a disk of dipoles with radius 0.8m and located at a distance of 0.8m from the electrode receiver line, plotted as a solid line in Figure 5b. The fit of this model to the data broadly indicates that the direct field is produced within a volume of earth of radius $\sim$0.8m. The absolute magnitude of the modeled dipole is entirely arbitrary; it is simply scaled to match the real data. The numerous variables that contribute to the real magnitude are too complex to permit exact modeling.

 

direct_amps
Figure 5 Direct field amplitudes. (a) Shot gather from Figure 2c, shown with bandpass filter 20 to 800 Hz. (b) Amplitude pattern for the direct field arrival at $\sim$0.005 seconds of gather in (a) plotted as dots, and modeled amplitudes as a solid line. Modeled amplitudes correspond with a disk of electric dipoles of radius 0.8m centered at 0.8m away from the electrode array.