




Next: DISPERSION RELATIONS FOR SEISMIC
Up: SINGULAR VALUE DECOMPOSITION FOR
Previous: Exact results for isotropic
Using the definitions of the Thomsen parameters, we can also rewrite the
terms appearing in (27) in order to make connection with
this related point of view. Recalling (5) and the fact that b = a - 2m, we have
| ![\begin{eqnarray}
{{a+b-c}\over{f}} \simeq 1 + {{3}\over{c-2l}}(c\delta + 4l\gamma)
+ {{4}\over{c-2l}}\left[c(\epsilon - \delta) - 4l\gamma\right],
\end{eqnarray}](img67.gif) |
(28) |
with some higher order corrections involving powers of 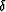 and products of
and products of 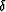 with
with  and
and 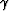 that we
neglected in this equation. We have added and subtracted equally
some terms proportional to
that we
neglected in this equation. We have added and subtracted equally
some terms proportional to 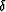 , and others proportional to
, and others proportional to
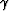 , in order to emphasize
the similarities between the form
(28)
and that found previously in (27). In particular, the
difference
, in order to emphasize
the similarities between the form
(28)
and that found previously in (27). In particular, the
difference 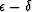 is known (Postma, 1955; Berryman, 1979)
to be non-negative and its deviations from zero depend on fluctuations
in
is known (Postma, 1955; Berryman, 1979)
to be non-negative and its deviations from zero depend on fluctuations
in 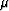 from layer to layer, behavior similar to that of
the final term in (27). Since the formula
(28) is only approximate and its interpretation
requires the use of various other results we derive subsequently for other
purposes, for now we will delay further discussion of this to a point
later in the paper. [See the discussion of Eq. (62).]
from layer to layer, behavior similar to that of
the final term in (27). Since the formula
(28) is only approximate and its interpretation
requires the use of various other results we derive subsequently for other
purposes, for now we will delay further discussion of this to a point
later in the paper. [See the discussion of Eq. (62).]





Next: DISPERSION RELATIONS FOR SEISMIC
Up: SINGULAR VALUE DECOMPOSITION FOR
Previous: Exact results for isotropic
Stanford Exploration Project
5/23/2004