




Next: Exact results for isotropic
Up: Berryman: Seismic waves in
Previous: Thomsen's
The singular value decomposition (SVD), or equivalently the eigenvalue
decomposition, of the real symmetric stiffness matrix appearing in
(1) is relatively easy to perform. We can immediately
write down four eigenvectors:
| 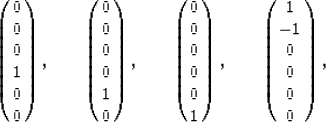 |
(20) |
and their corresponding eigenvalues, respectively
2l, 2l, 2m, and a-b = 2m. All four correspond to shear
modes of the system.
The two remaining eigenvectors must be orthogonal to all four of these
and therefore both must have the general form
| 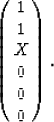 |
(21) |
Applying (21) to the stiffness
matrix in (1) shows that the corresponding eigenvalue is
| 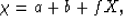 |
(22) |
where the remaining condition that determines both X and 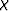 is
is
| 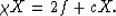 |
(23) |
After substitution for 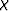 , we obtain a quadratic equation
having the solutions
, we obtain a quadratic equation
having the solutions
| ![\begin{eqnarray}
X_{\pm} = {{1}\over{2}}\left(-\left[{{a + b - c}\over{f}}\right]
\pm\sqrt{8 + \left[{{a + b - c}\over{f}}\right]^2}\right).
\end{eqnarray}](img56.gif) |
(24) |
The ranges of values for 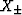 are
are
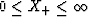 and, since X- = -2/X+,
and, since X- = -2/X+,
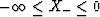 .The interpretation of the solutions
.The interpretation of the solutions
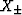 is simple for the isotropic limit
where X+ = 1 and X- = -2, corresponding respectively to
pure compression and pure shear modes. So, except for special angles
of propagation, these two modes always have mixed character,
indicating that pure compression cannot be
excited in the system, and must always be coupled to shear. Some
types of pure shear modes can still be excited even in the
nonisotropic cases, because the other four eigenvectors in
(20) are unaffected
by this coupling, and they are all pure shear modes. Pure compressional
and shear modes are obtained as linear combinations of these two mixed
modes according to
is simple for the isotropic limit
where X+ = 1 and X- = -2, corresponding respectively to
pure compression and pure shear modes. So, except for special angles
of propagation, these two modes always have mixed character,
indicating that pure compression cannot be
excited in the system, and must always be coupled to shear. Some
types of pure shear modes can still be excited even in the
nonisotropic cases, because the other four eigenvectors in
(20) are unaffected
by this coupling, and they are all pure shear modes. Pure compressional
and shear modes are obtained as linear combinations of these two mixed
modes according to
| 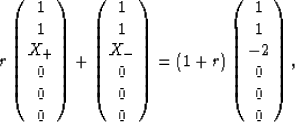 |
(25) |
with r = -2(X+-1)/[X+(X+ + 2)]
for pure shear, and
| 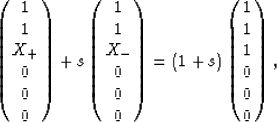 |
(26) |
with s = X+(X+ - 1)/(X+ + 2)
for pure compression.
To understand the behavior of X+ in terms of the layer
property fluctuations or, alternatively, in terms of the Thomsen
parameters, it is first helpful to note that the pertinent functional
![$F(x) = {{1}\over{2}}\left[-x + \sqrt{8 + x^2}\right]$](img62.gif) is easily shown
to be a monotonic function of its argument x. So it is sufficient
to study the behavior of the argument x = (a+b-c)/f.
is easily shown
to be a monotonic function of its argument x. So it is sufficient
to study the behavior of the argument x = (a+b-c)/f.


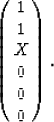
![\begin{eqnarray}
X_{\pm} = {{1}\over{2}}\left(-\left[{{a + b - c}\over{f}}\right]
\pm\sqrt{8 + \left[{{a + b - c}\over{f}}\right]^2}\right).
\end{eqnarray}](img56.gif)
![]() are
are
![]() and, since X- = -2/X+,
and, since X- = -2/X+,
![]() .The interpretation of the solutions
.The interpretation of the solutions
![]() is simple for the isotropic limit
where X+ = 1 and X- = -2, corresponding respectively to
pure compression and pure shear modes. So, except for special angles
of propagation, these two modes always have mixed character,
indicating that pure compression cannot be
excited in the system, and must always be coupled to shear. Some
types of pure shear modes can still be excited even in the
nonisotropic cases, because the other four eigenvectors in
(20) are unaffected
by this coupling, and they are all pure shear modes. Pure compressional
and shear modes are obtained as linear combinations of these two mixed
modes according to
is simple for the isotropic limit
where X+ = 1 and X- = -2, corresponding respectively to
pure compression and pure shear modes. So, except for special angles
of propagation, these two modes always have mixed character,
indicating that pure compression cannot be
excited in the system, and must always be coupled to shear. Some
types of pure shear modes can still be excited even in the
nonisotropic cases, because the other four eigenvectors in
(20) are unaffected
by this coupling, and they are all pure shear modes. Pure compressional
and shear modes are obtained as linear combinations of these two mixed
modes according to
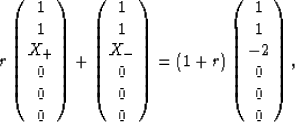
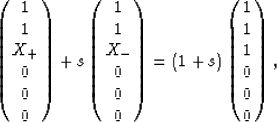
![]() is easily shown
to be a monotonic function of its argument x. So it is sufficient
to study the behavior of the argument x = (a+b-c)/f.
is easily shown
to be a monotonic function of its argument x. So it is sufficient
to study the behavior of the argument x = (a+b-c)/f.