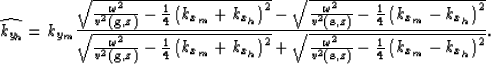
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
than in the narrow-azimuth migration results
(Figure
)
than in the narrow-azimuth migration results
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
but, as I discuss in Biondi (2001),
they might also become a problem
when narrow-azimuth downward-continuation
is used
with constant sampling in the cross-line offset wavenumber (dkyh).
A potential solution to the problem caused by
boundary effects can be the use of
absorbing boundary conditions.
However,
effective absorbing boundary conditions require the addition
of several grid points,
and consequently can cause a substantial increase in the computational cost.
),
but, as I discuss in Biondi (2001),
they might also become a problem
when narrow-azimuth downward-continuation
is used
with constant sampling in the cross-line offset wavenumber (dkyh).
A potential solution to the problem caused by
boundary effects can be the use of
absorbing boundary conditions.
However,
effective absorbing boundary conditions require the addition
of several grid points,
and consequently can cause a substantial increase in the computational cost.
Fortunately, the boundary artifacts can be effectively attenuated by applying a post-processing filter on the prestack image that preserves only the events for which the source and receiver rays are coplanar at the imaging point. This condition must be fulfilled by all the events that are correctly focused at zero offset because two lines passing through the same point are coplanar. The coplanarity condition can be easily applied on the prestack image after transformation into the Fourier domain, possibly at the same time that ADCIGs are computed using a 3-D generalization of the method described by Sava and Fomel (2003), as presented in Tisserant and Biondi (2003).
The coplanarity condition can be derived by simple geometric considerations starting from the common-azimuth condition expressed as Biondi and Palacharla (1996):
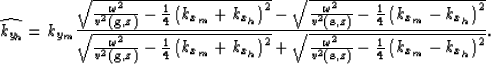 |
(1) |
As for the common-azimuth condition, the coplanarity condition can be expressed as a relationship that links the cross-line offset wavenumber kyh to the other wavenumbers in the image. For events with azimuth aligned along the in-line direction (xm in my notation), the expression of the coplanarity condition is:
| |
(2) |
The condition expressed in equation (2)
can be easily generalized to be valid
for an arbitrary azimuthal direction ![]() Tisserant and Biondi (2003).
The wavenumber axes are rotated by
Tisserant and Biondi (2003).
The wavenumber axes are rotated by ![]() in both the midpoint wavenumber plane
in both the midpoint wavenumber plane ![]() and the offset wavenumber plane
and the offset wavenumber plane ![]() .
.
As discussed in Tisserant and Biondi (2003),
in a prestack image
each event fulfills
the coplanarity condition
for one value of the azimuth.
However, streamer data illuminate the
reflectors only within a fairly narrow azimuthal range.
Therefore, the coplanarity condition
can be used to remove from the prestack image
all the events that are imaged outside a given
azimuthal range.
For example, if we image only
events within a range of ![]() degrees,
we will remove the 75 % of the events in the image
that are least likely to be real reflection events.
degrees,
we will remove the 75 % of the events in the image
that are least likely to be real reflection events.