Narrow-azimuth migration of marine streamer data

Biondo Biondi

biondo@sep.stanford.edu

ABSTRACT

I introduce a new migration method that overcomes the limitations of common-azimuth migration while retaining its computational efficiency for imaging marine streamer data. The method is based on source-receiver downward-continuation of prestack data with a narrow range of cross-line offsets. To minimize the width of the cross-line offset range, while assuring that all the recorded events are correctly propagated, I define an ``optimal'' range of cross-line offset dips. To remove the effects of the boundary artifacts I apply a coplanarity condition on the prestack image. This process removes from the image cube the events that are not correctly focused at zero offset. Tests of the proposed method with the SEG-EAGE salt dataset show substantial image improvements in particularly difficult areas of the model and thus confirm the capability of the new method to overcome the limitations of common-azimuth migration in complex areas.

Introduction Common-azimuth Biondi and Palacharla (1996) is an attractive alternative to shot-profile migration for wave-equation 3-D prestack migration. For 3-D marine streamer data, it is computationally more efficient than shot-profile migration and thus it has been implemented in different migration algorithms Jin et al. (2002) and applied to several datasets Fliedner et al. (2002); Le Rousseau et al. (2002). In addition to the computational efficiency, common-azimuth migration has the substantial advantage of enabling migration velocity analysis Clapp and Biondi (2000); Liu et al. (2001) by generating high-quality Angle-Domain Common Image Gathers (ADCIG) Prucha et al. (1999) without additional computations. However, in the presence of arbitrary velocity functions, common-azimuth migration is not exact. In this paper, I propose a method for generalizing common-azimuth migration that is accurate in presence of arbitrary velocity variations but retains computational advantages with respect to shot-profile migration.

Common-azimuth migration is based on the principles of source-receiver (survey-sinking) migration Claerbout (1985). Source-receiver migration is theoretically equivalent to shot-profile migration based on downward continuation Biondi (2002); Shan and Zhang (2003); Wapenaar and Berkhout (1987). (notice, not shot-profile migration based on time extrapolation), and thus the proposed generalization of common-azimuth migration has the potential to produce as high-quality images as the more computationally demanding shot-profile migration.

At the basis of common-azimuth computational efficiency is the exploitation of the narrow azimuthal range of typical marine data acquired by towed streamers. This is made possible by a crucial characteristic of source-receiver migration: during source-receiver downward continuation the offset range shrinks with depth. In most practical situations the offset range shrinks monotonically with depth, but this property is not guaranteed in arbitrarily heterogeneous media. At the limit, the cross-line offset can be assumed to be zero and all recorded events can be propagated with the same azimuth (e.g. common azimuth) at every depth level. The assumption of no cross-line offset provides the computational efficiency of common-azimuth migration, but also causes its accuracy limitations. In this paper I remove this assumption by downward continuing the data on a narrow, but finite, cross-line offset range. To achieve computational efficiency, the cross-line offset range must be as narrow as possible and still ``capture'' all the useful propagation paths and avoid boundary artifacts. I propose to accomplish this goal by applying two complementary procedures: 1) definition of an ``optimal'' range of cross-line offset dips for the downward continuation, and 2) application of a coplanarity condition on the prestack image that enhances the events that are well focused at the imaging point (zero offset). I presented a method to perform 1) in Biondi (2001). In this paper I introduce a method to perform 2).

Narrow-azimuth migration In Biondi (2001) I describe a method for reducing the cost of full prestack downward continuation in the midpoint-wavenumber domain by defining an ``optimal'' range of cross-line offset dips. The method exploits the information provided by the common-azimuth equation to define a range of cross-line offset wavenumbers. To illustrate the need for applying the coplanarity condition on the prestack image for enhancing the events that are well focused at the imaging point (zero offset), I will now review some of the results presented in my previous report. In that report I analyzed in detail the kinematics of the migration results of a 3-D synthetic data set Vaillant and Biondi (2000). The reflectivity field consists of a set of five dipping planes, from zero dip to 60 degrees dip. The azimuth of the planes is 45 degrees with respect to the direction of the acquisition. This reflection geometry (i.e. dipping reflectors oriented at 45 degrees with respect to the acquisition direction) is known to be the most challenging for common-azimuth migration. The velocity was $V\left(z\right)= 1.5 + .5 z$ km/s, which corresponds to the upper limit among the typical gradients found in the Gulf of Mexico. The maximum source-receiver offset was 3 km. Figure  shows the geometry of the reflectors.

Figure  shows a subset of the image cube obtained by common-azimuth migration. The front face of the cube displayed in the figure is an in-line section through the stack. The other two faces are sections through the prestack image as a function of the offset ray parameter p_xh. The three events in the ADCIG (right panel) correspond to the planes dipping at 30, 45 and 60 degrees. Notice that the events are almost perfectly flat as a function of the offset ray parameter p_xh, except for the reflections from the 60-degree plane with large offset ray parameters (i.e. large reflection angle). This slight smiling in the ADCIG is caused by the common-azimuth approximation.

The small error visible in the common-azimuth migration can be completely corrected by using full source-receiver migration. Figure  shows an ADCIG extracted at the same location as the ADCIG shown in Figure , but from the migrated image obtained by a full source-receiver migration. For these data, 16 cross-line offsets were necessary to obtain an accurate image when using full source-receiver migration. In contrast, only 4 cross-line offsets are necessary to obtain an accurate image when using the narrow-azimuth downward continuation described in Biondi (2001). Figure  shows an ADCIG extracted at the same location as the ADCIG shown in Figure , but from the migrated image obtained by narrow-azimuth migration with N_yh=4.

 

planes Figure 1 Geometry of the set of slanted planes, dipping at 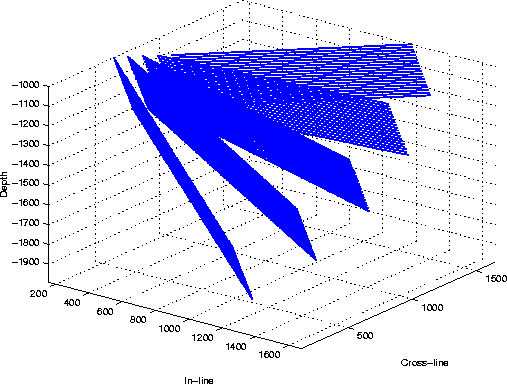$0^\circ$, $15^\circ$, $30^\circ$, $45^\circ$ and $60^\circ$ toward increasing x and y, at $45^\circ$ with respect to the in-line direction.

 

CA-pull-WKBJ-stat-vp-vp Figure 2 Subset of the results of common-azimuth migration of the synthetic data set. The front face of the cube is an in-line section through the stack. The other two faces are sections through the prestack image.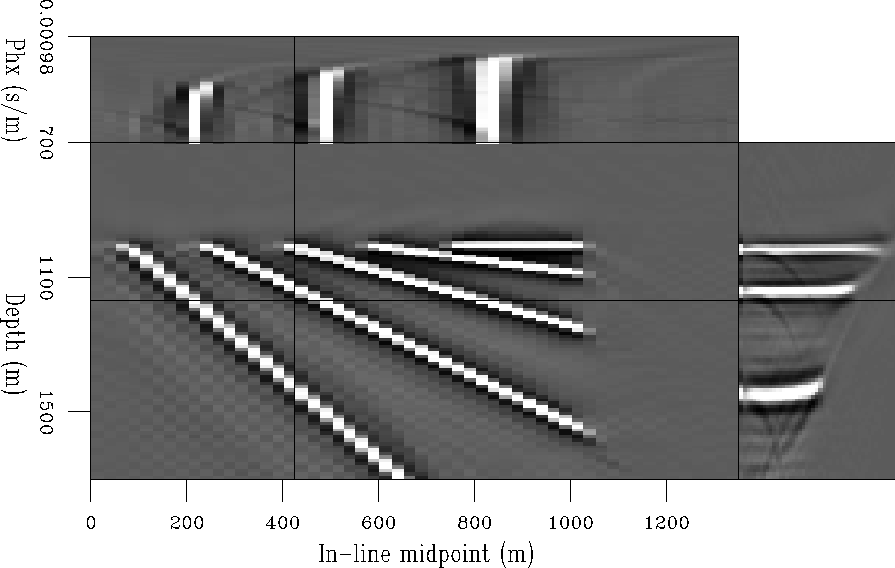

 

CIG-PS-16-nhy-WKBJ Figure 3 ADCIG extracted at the same location as the ADCIG shown in Figure , but from the migrated image obtained by a full source-receiver migration with Nyh=16.

 

CIG-NA-4-nhy-WKBJ Figure 4 ADCIG extracted at the same location as the ADCIG shown in Figure , but from the migrated image obtained by narrow-azimuth migration with Nyh=4.