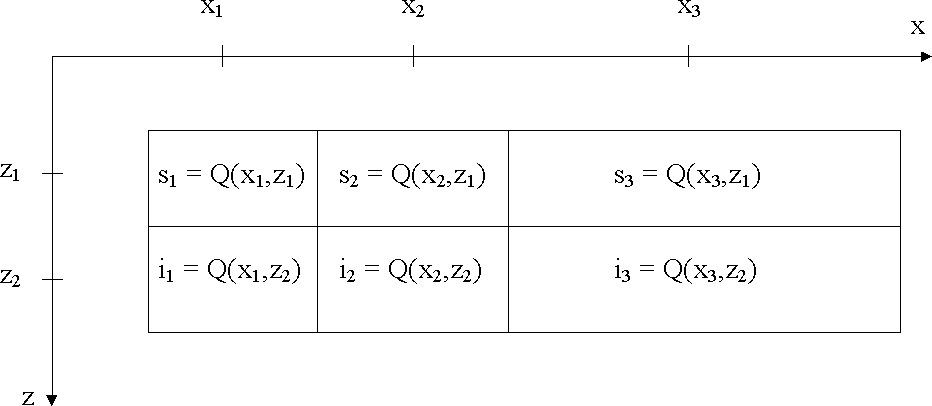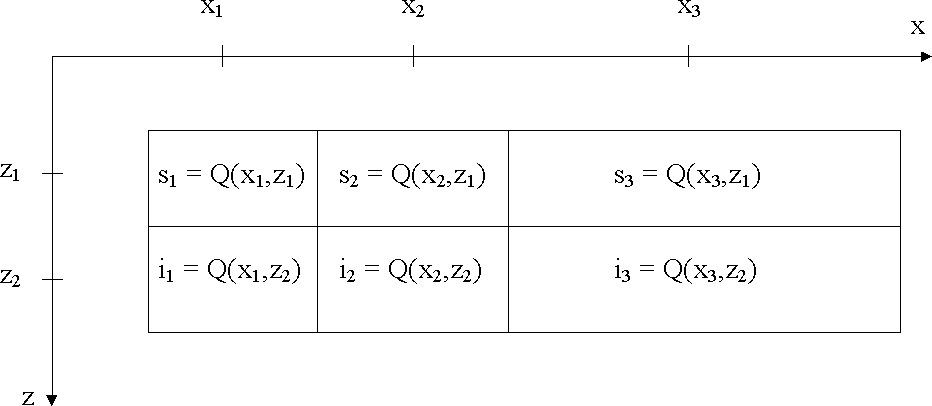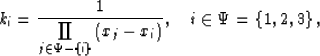Next: Implementation of a 2D,
Up: Vlad: Irregular data migration
Previous: SMM advantages and disadvantages
Let 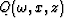 denote a 2D zero-offset seismic
wavefield, regularly sampled (and Fourier transformed) in time,
but irregularly sampled in space. The measured surface dataset is
denote a 2D zero-offset seismic
wavefield, regularly sampled (and Fourier transformed) in time,
but irregularly sampled in space. The measured surface dataset is 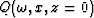 . For downward continuing Q with (1) we
need to write differencing stars for
. For downward continuing Q with (1) we
need to write differencing stars for 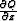 and for
and for 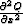 . Fig. 1 shows the differencing star for the
entire equation and defines shorthand
notations.
. Fig. 1 shows the differencing star for the
entire equation and defines shorthand
notations.
diffstar
Figure 1 Differencing
star for solving eq. 1 with the finite difference method; s1,
s2, s3, i1, i2, i3 are just notations. This is the
general case: the distance x2 - x1 is not necessarily equal to
x3 - x2.
|
| 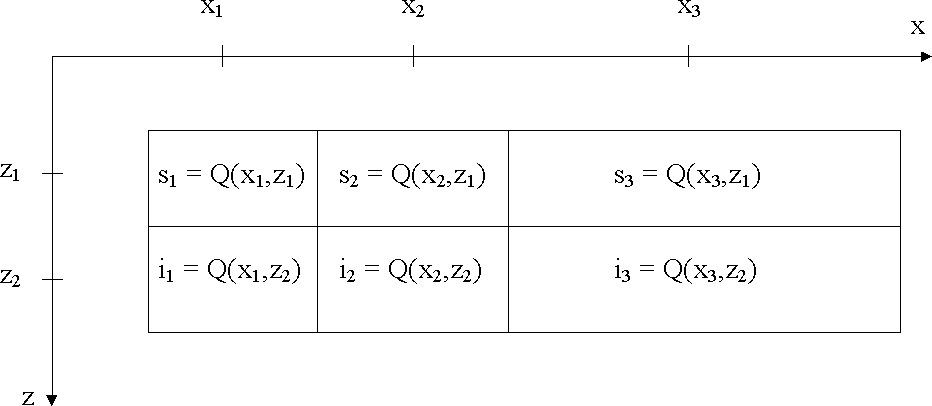 |
 Since the differencing star spans only two values of z,
it does not matter whether the sampling along the z axis is regular or
not. I denote:
Since the differencing star spans only two values of z,
it does not matter whether the sampling along the z axis is regular or
not. I denote:
| 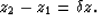 |
(2) |
All derivatives will be considered to be computed in the middle of the
differencing star. When x2 - x1 = x3 - x2, the middle is in
x2. When the two distances are drastically different, the middle is
not in x2 any more and errors are introduced. This may be the cause
of the spurious reflections off the large variations in grid steps
that are visible in the bottom panel of
Fig. 4. Dellinger and Muir (1986) discuss
this problem and suggest that letting the gridpoints drift across x
as we downward continue can solve it. In order to examine the extent
to which this problem affects the data, I will simply pretend that the
problem does not exist, and observe its negative effects. So, given the values
of a function y(x) in three points, x1, x2 and x3, with
x1 < x2 < x3, the second derivative can be computed by finding
the coefficients of parabola that fits through the three points. The
second derivative is twice the coefficient of the second-degree term
in the parabola expression. Thus, by denoting:
| 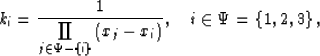 |
(3) |
which can be more explicitly written out as
| 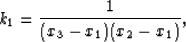 |
(4) |
| 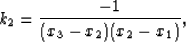 |
(5) |
| 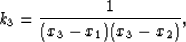 |
(6) |
the second derivative is
| 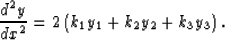 |
(7) |
The same formula is obtained by computing a first-order
approximation of the second derivative as the first derivative of the
first derivative in the point x2. It should be noticed that the
Laplacian is a low-pass filter of the original functionr. In other
words, the curvature of the hyperbola is the same in each of the
three points it fits through; x3 - x2 must be really different
from x2 - x1 in order for the curvature-fitting hyperbola to be
affected by the error and for artifacts to be generated. This explains
why the method is so robust. As Fig. 3 shows, artifacts
start to become barely visible when x3 - x2 = 2(x2 - x1). The
partial derivatives in x of even order higher than two of the
wavefield will be even more robust. A method that would make
use not of the second-order derivatives but of the fourth-order ones,
would be much less affected by the spurious reflections.
Using the notations in Fig. 1 and
eq. (2), the second derivative expression in
(7), and employing a Crank-Nicolson scheme to
compute the second derivative in x, we obtain the following
differencing stars:
| 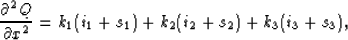 |
(8) |
| 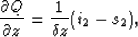 |
(9) |
| 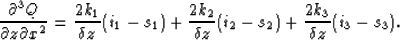 |
(10) |
The way the derivatives of a function are computed on a
irregular mesh does not depend on the nature of the
function, but the result of the computation does: the lower the frequency
content, the better. This means that longer wavelengths will generate
less artifacts, and the spatio-temporal frequency content of the
spurious reflections will therefore be biased towards the high part of
the spectrum. Practically no artifacts should be produced when the
function has a very low frequency content, as is the case with
potential fields. Upward or downward continuation of potential fields
on a unstructured mesh should be very accurate.





Next: Implementation of a 2D,
Up: Vlad: Irregular data migration
Previous: SMM advantages and disadvantages
Stanford Exploration Project
6/8/2002