SMM results - presentation and discussion

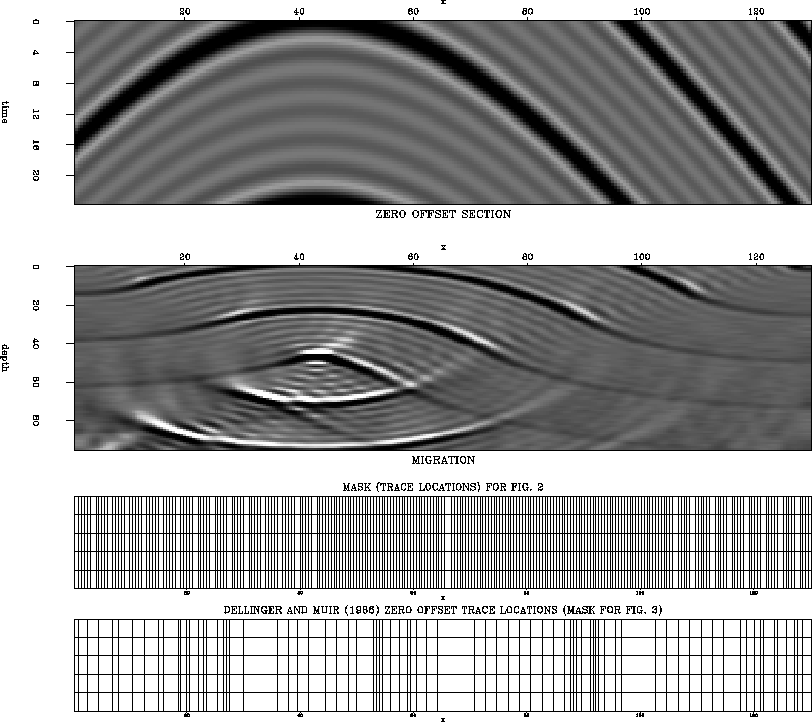
I examined the SMM results on a simple synthetic dataset. I chose the one in Claerbout (1999) because it was small, simple, and the migration result was already known. First, I produced a surrogate irregular dataset - a zero offset section that was densely and regularly sampled across the x axis (see Fig. 2, upper panel). The image was migrated with the SMM code, as if it were a irregularly sampled dataset. Only the numerical values of the traces' coordinates were making it regular; the code was the same as for the truly irregular cases. The result is displayed in the middle panel of Fig. 2. The input data was ``made'' irregular by applying masks (shown in the bottom part of Fig. 2). SMM was performed on the traces present in the mask. For comparison, zero traces were introduced at the locations that were not present in the masks and surrogate irregular migration was performed.

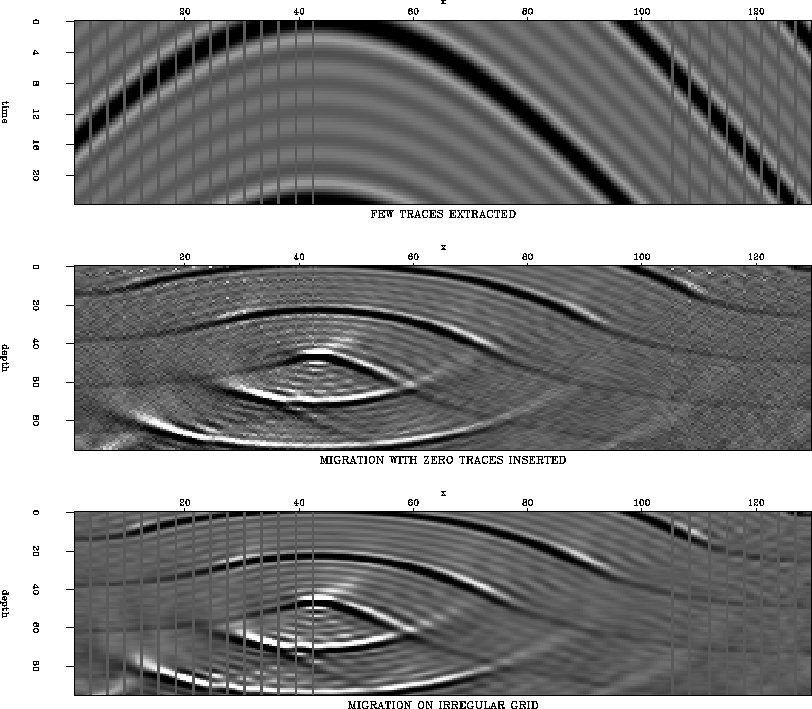
Fig. 3 shows the input data (top panel), the zero-traces inserted migration (middle panel) and the SMM (bottom panel). The irregularity introduced by the mask is mild (the sixth trace has been eliminated in two regions). Inserting zero traces and imaging on a regular grid introduces noise farther away from the missing traces as depth increases. Overall, the image is full of incoherent high-frequency noise. Instead, the SMM result introduces no such problems. Even if the jump in sampling rate is large at the place of the missing traces (the step becomes 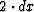$2 \cdot dx$ instead of dx), the reflections off the side of the grid are minor. This makes me believe that for jumps in the grid step of the order of half of dx and under, the artifacts would be negligible.

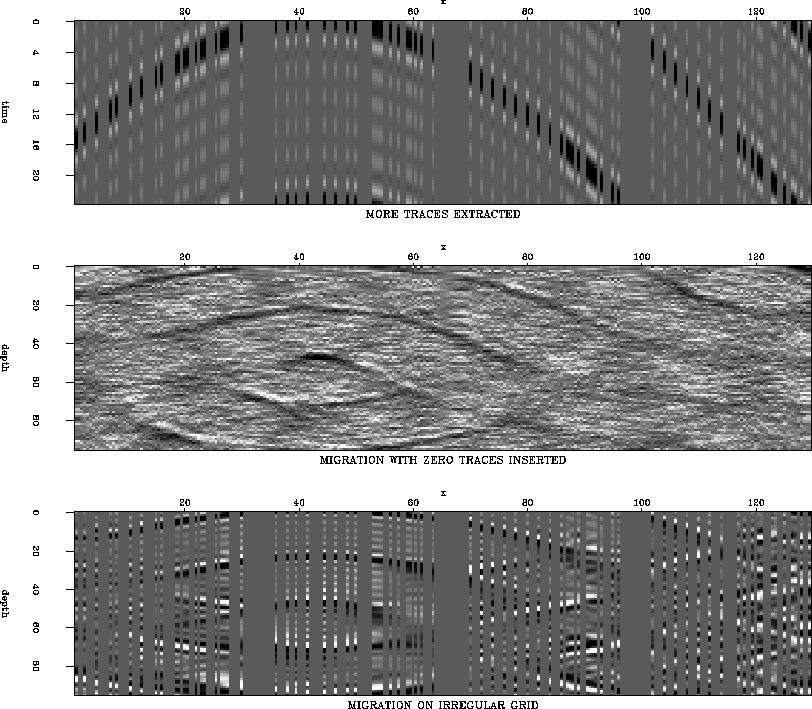
Fig. 4 shows the effect of severe irregularities. Both images are severely affected. The S/N ratio of the zero-traces inserted surrogate irregular migration result is lowered to the limit of interpretablity, and any mistake while interpolating the traces (if we interpolate instead of inserting zero traces) would probably have severe effects as well. The SMM result is plagued by strong spurious reflections, but we notice that these are: a) localized, and b) highly coherent and dipping in the opposite direction from the true local dips. These are prone to filtering with a reasonable apriori assumption about the direction of the dip, and can be obtained as well from unmigrated data. The SMM image overall is crisp and interpretable. The fact that the incoherent noise has not been increased is particularly important because input datasets already suffer from a S/N problem, such as those in crustal seismology.

 

init
Figure 2 Input data from Claerbout (1999), its surrogate irregular 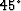$45^\circ$migration and the sampling masks used for creating irregularly sampled datasets

 

midtk
Figure 3 Input data (top panel), migration with zero-traces inserted (middle panel) and the SMM (bottom panel)

 

reflgrid
Figure 4 Input data (top panel), migration with zero-traces inserted (middle panel) and the SMM (bottom panel)