Introduction

Common sense and basic physics suggest that in order to continue a field (gravitational, magnetic, wavefield) into a direction, it is necessary to know the values of the field on one or more surfaces nonparallel to the continuation direction, and the law that governs the field (approximations can be made or field laws inferred so that we need only one surface). Because field quantities are usually invariants, nothing mandates that field continuations be done on Cartesian grids (although in many cases it is numerically convenient to do so). In particular, a look at the 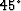$45^\circ$ downward continuation equation Claerbout (1999) shows that it can be written as:

 

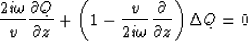$$\frac{{2i\omega }}{v}\frac{{\partial Q}}{{\partial z}} + \le... ...{2i\omega }}\frac{\partial }{{\partial z}}} \right)\Delta Q = 0$$ (1)

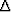where $\Delta$Q, the Laplacian of Q, is an invariant. It can also be computed on an unstructured spatial mesh. In principle, this means that semistructured mesh migration (SMM) is feasible. I called the mesh semistructured because it is regular in time, but unstructured in space.