Devil's Advocate: What do the Multiples Add?

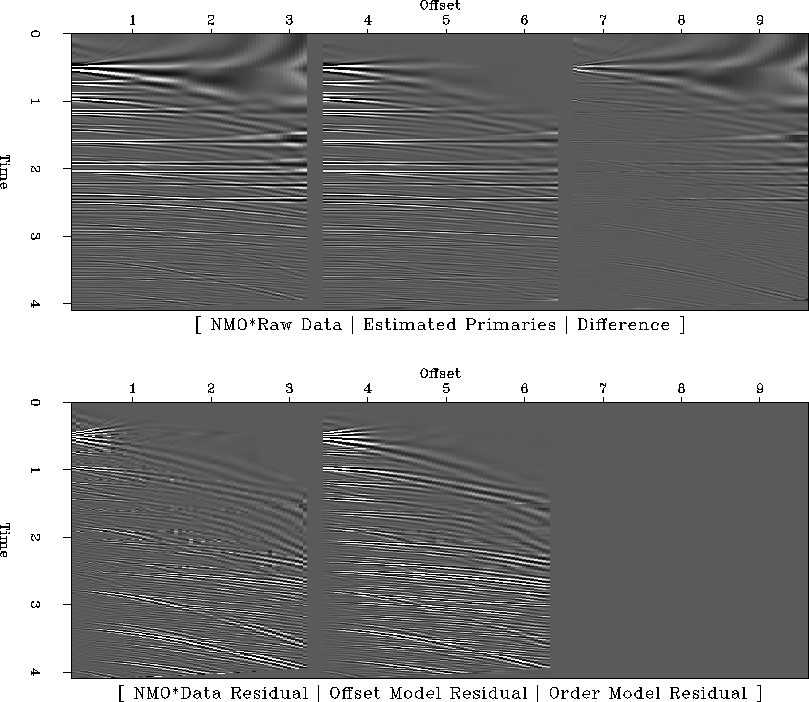
Figure 6 illustrates application of the algorithm without the use of multiples. Only the regularization across offset, equation (9), is in operation. Though we see some suppression of multiples, the results are not nearly as good as those in Figure 4. More insidiously, note the presence of considerable of primary energy in the difference panel. When exploited as a constraint against crosstalk, the multiple reflections add considerable information. My approach integrates this information in a systematic framework.

 

cmps.devils.hask
Figure 6 Only the regularization which roughens across offset, equation (9) is used in the inversion. Only one order of pseudo-primary is used, so no information is added by the multiples. Top row, left to right: Raw Haskell data, NMO applied; Estimated primary panel; difference panel. Bottom row, left to right: Data residual; first panel of model residuals, equations (9) and (8), respectively.