




Next: True-amplitude shot-modeling
Up: Shot-profile migration and modeling
Previous: Exploding-reflector modeling by upward
Shot-profile migration is similar to exploding-reflector
migration, except individual shot records are migrated independently.
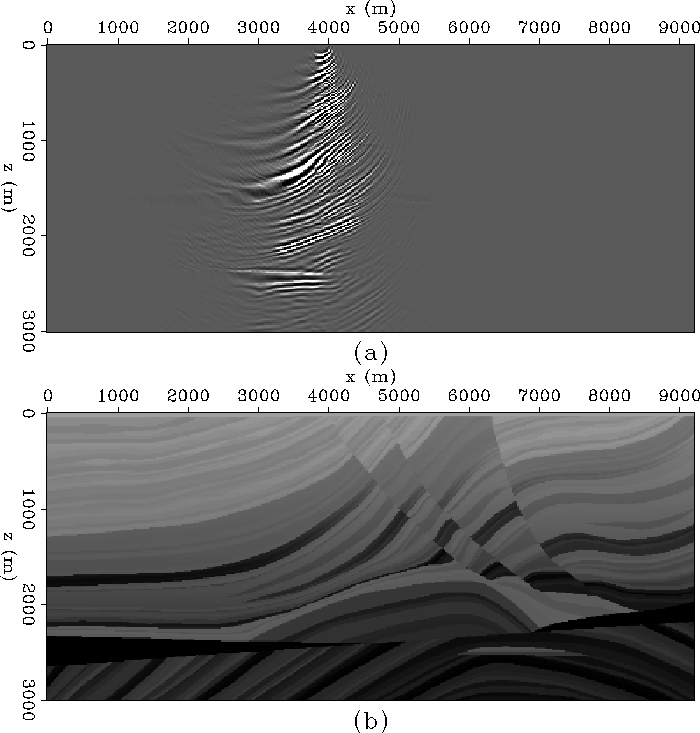
Single shot-record migrations (like Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are
then stacked to provide a complete reflectivity image.
) are
then stacked to provide a complete reflectivity image.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Rather than downward-continue a single wavefield into the earth,
we downward-continue two wavefields simultaneously (but still one
frequency at a time).
Firstly, there is upgoing wavefield (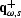 ), which
was recorded on the surface as the shot-gather,
), which
was recorded on the surface as the shot-gather, 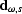 ,with a shot at s. The equation for downward continuing this
wavefield is:
,with a shot at s. The equation for downward continuing this
wavefield is:
| 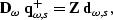 |
(71) |
Secondly, there is the downgoing wavefield (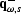 ),
),
| 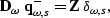 |
(72) |
which we did not record on the surface but we can
simulate as an impulse at the shot
location, 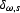 .
.
To image an individual shot, we crosscorrelate the two wavefields and
extract the image at zero-time, or equivalently multiply their Fourier
coefficients and sum over frequencies.
The matrix operation described by this process is,
| 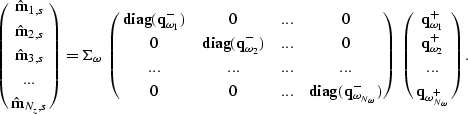 |
(73) |
To image the entire survey we then stack over shot-location.
Full prestack shot-profile migration is therefore described by the
equation
| 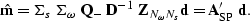 |
(74) |
where 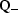 =
= 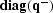 , and
, and
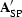 is the composite shot-profile migration operator.
is the composite shot-profile migration operator.
The adjoint of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes a process of
common-shot modeling:
) describes a process of
common-shot modeling:
| 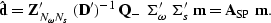 |
(75) |
Implementing equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is slightly more difficult
than equation (
) is slightly more difficult
than equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), since we cannot downward continue
both wavefields from the surface simultaneously.
However, we can still work with frequency slices; although for each
frequency we must downward continue the shot wavefield from the
surface to the bottom of the model storing it as we go, and then
upward continue the reflected wavefield to the surface.
), since we cannot downward continue
both wavefields from the surface simultaneously.
However, we can still work with frequency slices; although for each
frequency we must downward continue the shot wavefield from the
surface to the bottom of the model storing it as we go, and then
upward continue the reflected wavefield to the surface.





Next: True-amplitude shot-modeling
Up: Shot-profile migration and modeling
Previous: Exploding-reflector modeling by upward
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are
then stacked to provide a complete reflectivity image.
) are
then stacked to provide a complete reflectivity image.

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![]() ), which
was recorded on the surface as the shot-gather,
), which
was recorded on the surface as the shot-gather, ![]() ,with a shot at s. The equation for downward continuing this
wavefield is:
,with a shot at s. The equation for downward continuing this
wavefield is:
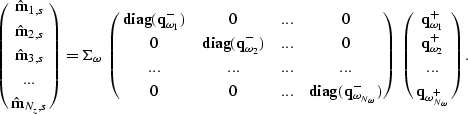
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes a process of
common-shot modeling:
) describes a process of
common-shot modeling:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is slightly more difficult
than equation (
) is slightly more difficult
than equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), since we cannot downward continue
both wavefields from the surface simultaneously.
However, we can still work with frequency slices; although for each
frequency we must downward continue the shot wavefield from the
surface to the bottom of the model storing it as we go, and then
upward continue the reflected wavefield to the surface.
), since we cannot downward continue
both wavefields from the surface simultaneously.
However, we can still work with frequency slices; although for each
frequency we must downward continue the shot wavefield from the
surface to the bottom of the model storing it as we go, and then
upward continue the reflected wavefield to the surface.