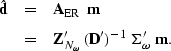Next: Shot-profile migration and modeling
Up: Shot-profile migration and modeling
Previous: Exploding-reflector migration by downward
The adjoint![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) of exploding-reflector migration is exploding-reflector modeling: if
we can migrate exploding-reflector data with
of exploding-reflector migration is exploding-reflector modeling: if
we can migrate exploding-reflector data with
| 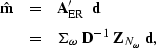 |
|
| (69) |
then we should be able to forward model synthetic data with
| 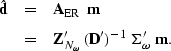 |
|
| (70) |
A close look at the composite operator reveals that the first step is
to apply 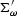 , which sprays the reflectivity model out to
each frequency. The second step is to apply
, which sprays the reflectivity model out to
each frequency. The second step is to apply 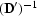 which
recursively marches the wavefield up through the earth. The final step
is to truncate the data at the surface with the
which
recursively marches the wavefield up through the earth. The final step
is to truncate the data at the surface with the 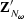 operator.
operator.





Next: Shot-profile migration and modeling
Up: Shot-profile migration and modeling
Previous: Exploding-reflector migration by downward
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) of exploding-reflector migration is exploding-reflector modeling: if
we can migrate exploding-reflector data with
of exploding-reflector migration is exploding-reflector modeling: if
we can migrate exploding-reflector data with