




Next: Towards true-amplitude migration
Up: Shot-profile migration and modeling
Previous: Shot-profile migration and modeling
Under the single-scattering (first-order Born) approximation the
scattered field at r due to a shot at s is given by
| 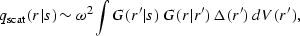 |
(76) |
where G(r|s) is the Green's function response at r of the medium
to an impulse at s, and 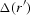 represents perturbation in
medium parameters.
represents perturbation in
medium parameters.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes the process of calculating the
volume integral in equation (
) describes the process of calculating the
volume integral in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) first by downward
continuing the shot wavefield to give G(r'|s), then by upward
continuing the scattered field to the surface, accumulating
contributions from each depth slice on the way back up. The
) first by downward
continuing the shot wavefield to give G(r'|s), then by upward
continuing the scattered field to the surface, accumulating
contributions from each depth slice on the way back up. The 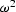 term can be applied as a data-space filter after modeling.
However, for the amplitudes to be correct in
equation (
term can be applied as a data-space filter after modeling.
However, for the amplitudes to be correct in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the extrapolation operators need to
represent true-amplitude Green's functions.
), the extrapolation operators need to
represent true-amplitude Green's functions.
For v(z) media, the WKBJ Green's function for a smoothly-varying
background velocity field [e.g. Aki and Richards (1980); Stolt and Benson (1986)] is
given by
| ![\begin{displaymath}
q(k_x,k_y,z_2,\omega) = q(k_x,k_y,z_1,\omega) \;
\sqrt{\frac...
...(z_2)}} \;
\exp \left[
i \int_{z_1}^{z_2} k_z(z') dz'
\right], \end{displaymath}](img184.gif) |
(77) |
| 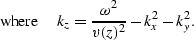 |
(78) |
The amplitude term in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be
incorporated into the shot-profile modeling procedure;
however, different operators are required for upward versus downward
continuation. Firstly, the true-amplitude downgoing WKBJ
extrapolators should be substituted into
equation (
) can be
incorporated into the shot-profile modeling procedure;
however, different operators are required for upward versus downward
continuation. Firstly, the true-amplitude downgoing WKBJ
extrapolators should be substituted into
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and secondly, the upgoing WKBJ extrapolators should be substituted for
the adjoint of
),
and secondly, the upgoing WKBJ extrapolators should be substituted for
the adjoint of 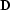 in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).





Next: Towards true-amplitude migration
Up: Shot-profile migration and modeling
Previous: Shot-profile migration and modeling
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes the process of calculating the
volume integral in equation (
) describes the process of calculating the
volume integral in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) first by downward
continuing the shot wavefield to give G(r'|s), then by upward
continuing the scattered field to the surface, accumulating
contributions from each depth slice on the way back up. The
) first by downward
continuing the shot wavefield to give G(r'|s), then by upward
continuing the scattered field to the surface, accumulating
contributions from each depth slice on the way back up. The ![]() term can be applied as a data-space filter after modeling.
However, for the amplitudes to be correct in
equation (
term can be applied as a data-space filter after modeling.
However, for the amplitudes to be correct in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the extrapolation operators need to
represent true-amplitude Green's functions.
), the extrapolation operators need to
represent true-amplitude Green's functions.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be
incorporated into the shot-profile modeling procedure;
however, different operators are required for upward versus downward
continuation. Firstly, the true-amplitude downgoing WKBJ
extrapolators should be substituted into
equation (
) can be
incorporated into the shot-profile modeling procedure;
however, different operators are required for upward versus downward
continuation. Firstly, the true-amplitude downgoing WKBJ
extrapolators should be substituted into
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
and secondly, the upgoing WKBJ extrapolators should be substituted for
the adjoint of
),
and secondly, the upgoing WKBJ extrapolators should be substituted for
the adjoint of ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).