Next: Multidimensional recursive filter preconditioning
Up: One-dimensional synthetic examples
Previous: One-dimensional synthetic examples
One of the factors affecting the convergence of iterative data
regularization is clustering of data points in the output bins. Since
least-squares optimization assigns equal weight to each data point, it
may apply inadequate effort to fit a cluster of data points with
similar values in a particular output bin. To avoid this problem, we
can replace the regularized optimization with a less accurate but more
efficient two-step approach: data binning followed by missing data
interpolation.
Missing data interpolation is a particular case of data
regularization, where the input data are already given on a regular
grid, and we need to reconstruct only the missing values in empty
bins. Claerbout (1992) formulates the basic
principle of missing data interpolation as follows:
A method for restoring missing data is to ensure that the restored
data, after specified filtering, has minimum energy.
Mathematically, this principle can be expressed by the simple
equation
| 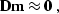 |
(73) |
where 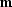 is the data vector and
is the data vector and 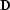 is the specified
filter. Equation (
is the specified
filter. Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is completely equivalent to
equation (
) is completely equivalent to
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The approximate equality sign means that
equation (
). The approximate equality sign means that
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is solved by minimizing the squared norm
(the power) of its left side. Additionally, the known data values
must be preserved in the optimization scheme. Introducing the mask
operator
) is solved by minimizing the squared norm
(the power) of its left side. Additionally, the known data values
must be preserved in the optimization scheme. Introducing the mask
operator 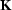 , which can be considered as a diagonal matrix with
zeros at the missing data locations and ones elsewhere, we can rewrite
equation (
, which can be considered as a diagonal matrix with
zeros at the missing data locations and ones elsewhere, we can rewrite
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the extended form
) in the extended form
| 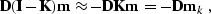 |
(74) |
in which 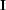 is the identity operator, and
is the identity operator, and 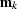 represents the known portion of the data. It is important to note that
equation (
represents the known portion of the data. It is important to note that
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) corresponds to the limiting case of the
regularized linear system
) corresponds to the limiting case of the
regularized linear system
| 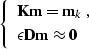 |
(75) |
for the scaling coefficient  approaching zero.
System (
approaching zero.
System (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is equivalent to
system (
) is equivalent to
system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the masking
operator
) with the masking
operator 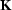 playing the role of the forward interpolation
operator
playing the role of the forward interpolation
operator 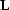 . Setting
. Setting  to zero implies putting far
more weight on the first equation in (
to zero implies putting far
more weight on the first equation in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and using the
second equation only to constrain the null space of the solution.
Applying the general theory of data-space regularization from
Chapter
) and using the
second equation only to constrain the null space of the solution.
Applying the general theory of data-space regularization from
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we can immediately transform system
(
, we can immediately transform system
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the equation
) to the equation
| 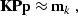 |
(76) |
where 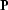 is a preconditioning operator, and
is a preconditioning operator, and 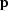 is the
preconditioning variable, connected with
is the
preconditioning variable, connected with 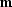 by the simple
relationship
by the simple
relationship
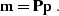
According to equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) from
Chapter
) from
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , equations (
, equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) have exactly the same solutions if the following
condition is satisfied:
) have exactly the same solutions if the following
condition is satisfied:
| 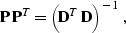 |
(77) |
where we need to assume the self-adjoint operator
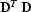 to be invertible. If
to be invertible. If 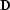 is represented
by a discrete convolution, the natural choice for
is represented
by a discrete convolution, the natural choice for 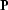 is the
corresponding deconvolution (inverse recursive filtering) operator:
is the
corresponding deconvolution (inverse recursive filtering) operator:
| 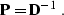 |
(78) |
I illustrate the missing data problem with a simple 1-D synthetic data
test taken from Claerbout (1999). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the
interpolation results of the unpreconditioned technique with three
different filters. For comparison with the preconditioned scheme, I
changed the boundary convolution conditions from internal to truncated
transient convolution. As in the previous example, the system was
solved with a conjugate-gradient iterative optimization.
shows the
interpolation results of the unpreconditioned technique with three
different filters. For comparison with the preconditioned scheme, I
changed the boundary convolution conditions from internal to truncated
transient convolution. As in the previous example, the system was
solved with a conjugate-gradient iterative optimization.
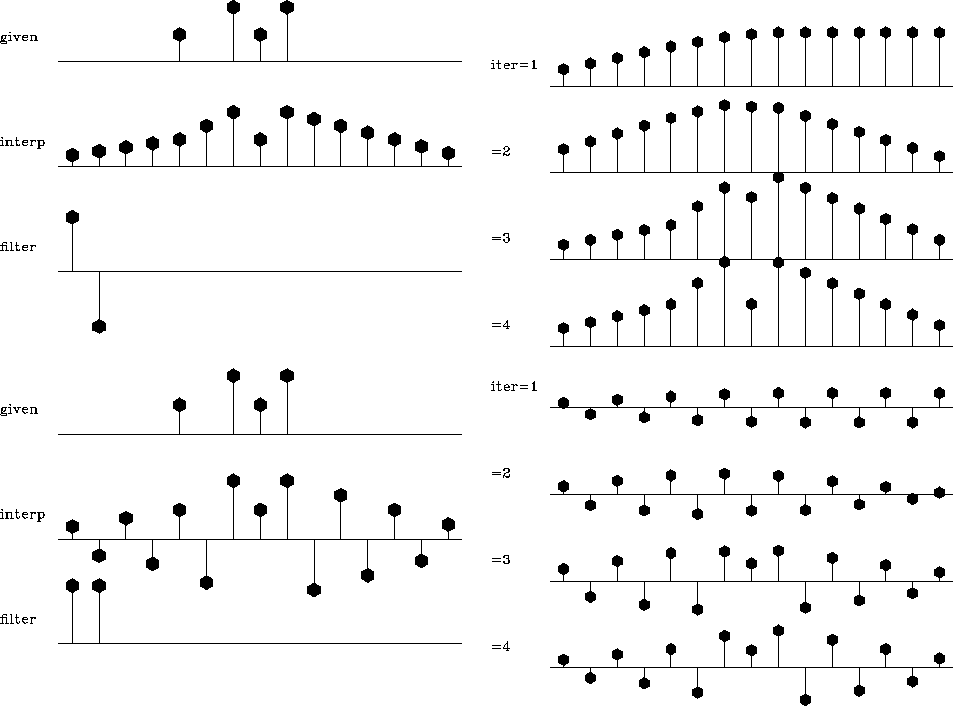
mall
Figure 8 Unpreconditioned
interpolation with two different regularization filters. Left plot:
the top shows the input data; the middle, the result of
interpolation; the bottom, the filter. The right plot shows the
convergence process for the first four iterations.





As depicted on the right side of the figures, the interpolation
process starts with a ``complicated'' model and slowly ``simplifies''
it until the final result is achieved.
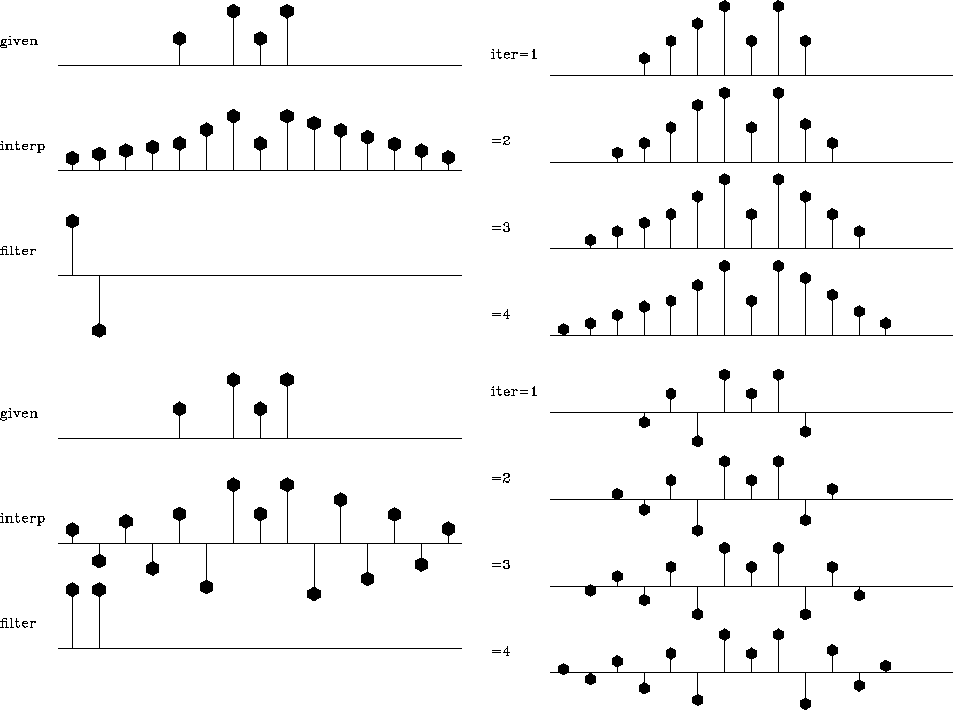
Preconditioned interpolation (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) behaves
differently. At the early iterations, the model is simple. As the
iteration proceeds, new details are added into the model. After a
surprisingly small number of iterations, the output closely resembles
the final output. The final output of interpolation with recursive
deconvolution preconditioning is exactly the same as that of the
original method.
) behaves
differently. At the early iterations, the model is simple. As the
iteration proceeds, new details are added into the model. After a
surprisingly small number of iterations, the output closely resembles
the final output. The final output of interpolation with recursive
deconvolution preconditioning is exactly the same as that of the
original method.
sall
Figure 9 Interpolation with
preconditioning. Left plot: the top shows the input data; the
middle, the result of interpolation; the bottom, the filter. The
right plot shows the convergence process for the first four
iterations.





The next section extends the idea of preconditioning by inverse
recursive filtering to multiple dimensions.





Next: Multidimensional recursive filter preconditioning
Up: One-dimensional synthetic examples
Previous: One-dimensional synthetic examples
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is completely equivalent to
equation (
) is completely equivalent to
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The approximate equality sign means that
equation (
). The approximate equality sign means that
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is solved by minimizing the squared norm
(the power) of its left side. Additionally, the known data values
must be preserved in the optimization scheme. Introducing the mask
operator
) is solved by minimizing the squared norm
(the power) of its left side. Additionally, the known data values
must be preserved in the optimization scheme. Introducing the mask
operator ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the extended form
) in the extended form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) corresponds to the limiting case of the
regularized linear system
) corresponds to the limiting case of the
regularized linear system
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is equivalent to
system (
) is equivalent to
system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the masking
operator
) with the masking
operator ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and using the
second equation only to constrain the null space of the solution.
Applying the general theory of data-space regularization from
Chapter
) and using the
second equation only to constrain the null space of the solution.
Applying the general theory of data-space regularization from
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , we can immediately transform system
(
, we can immediately transform system
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the equation
) to the equation
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) from
Chapter
) from
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , equations (
, equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) have exactly the same solutions if the following
condition is satisfied:
) have exactly the same solutions if the following
condition is satisfied:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the
interpolation results of the unpreconditioned technique with three
different filters. For comparison with the preconditioned scheme, I
changed the boundary convolution conditions from internal to truncated
transient convolution. As in the previous example, the system was
solved with a conjugate-gradient iterative optimization.
shows the
interpolation results of the unpreconditioned technique with three
different filters. For comparison with the preconditioned scheme, I
changed the boundary convolution conditions from internal to truncated
transient convolution. As in the previous example, the system was
solved with a conjugate-gradient iterative optimization.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) behaves
differently. At the early iterations, the model is simple. As the
iteration proceeds, new details are added into the model. After a
surprisingly small number of iterations, the output closely resembles
the final output. The final output of interpolation with recursive
deconvolution preconditioning is exactly the same as that of the
original method.
) behaves
differently. At the early iterations, the model is simple. As the
iteration proceeds, new details are added into the model. After a
surprisingly small number of iterations, the output closely resembles
the final output. The final output of interpolation with recursive
deconvolution preconditioning is exactly the same as that of the
original method.