




Next: Data-space regularization (model preconditioning)
Up: Data regularization as an
Previous: Data regularization as an
Model-space regularization implies adding equations to system
| 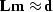 |
(15) |
to obtain a fully constrained (well-posed) inverse problem. The
additional equations take the form
| 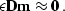 |
(16) |
The full system of equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be
written in a short notation as
) can be
written in a short notation as
| ![\begin{displaymath}
\bold{G_m m} = \left[\begin{array}
{c} \bold{L} \\ \epsilon...
... \bold{d} \\ \bold{0} \end{array}\right] =
\hat{\bold{d}}\;,\end{displaymath}](img44.gif) |
(17) |
where 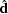 is the effective data vector:
is the effective data vector:
| ![\begin{displaymath}
\hat{\bold{d}} = \left[\begin{array}
{c} \bold{d} \\ \bold{0}
\end{array}\right]\;,\end{displaymath}](img46.gif) |
(18) |
and 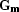 is a column operator:
is a column operator:
| ![\begin{displaymath}
\bold{G_m} = \left[\begin{array}
{c} \bold{L} \\ \epsilon \bold{D}
\end{array}\right]\;.\end{displaymath}](img48.gif) |
(19) |
The estimation problem (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is fully constrained. We can
solve it by means of unconstrained least-squares optimization,
minimizing the squared power
) is fully constrained. We can
solve it by means of unconstrained least-squares optimization,
minimizing the squared power 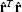 of the
compound residual vector
of the
compound residual vector
| ![\begin{displaymath}
\hat{\bold{r}} = \hat{\bold{d}} - \bold{G_m m} =
\left[\begi...
... \bold{d - L m}\\ - \epsilon \bold{D m}
\end{array}\right]\;.\end{displaymath}](img50.gif) |
(20) |
The formal solution of the regularized optimization problem has a
known form, which coincides with formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). One can
carry out the optimization iteratively with the help of the
conjugate-gradient method Hestenes and Steifel (1952) or its analogs
Paige and Saunders (1982).
). One can
carry out the optimization iteratively with the help of the
conjugate-gradient method Hestenes and Steifel (1952) or its analogs
Paige and Saunders (1982).
The next subsection introduces an alternative formulation of the
optimization problem.





Next: Data-space regularization (model preconditioning)
Up: Data regularization as an
Previous: Data regularization as an
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be
written in a short notation as
) can be
written in a short notation as
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is fully constrained. We can
solve it by means of unconstrained least-squares optimization,
minimizing the squared power
) is fully constrained. We can
solve it by means of unconstrained least-squares optimization,
minimizing the squared power ![]() of the
compound residual vector
of the
compound residual vector
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). One can
carry out the optimization iteratively with the help of the
conjugate-gradient method Hestenes and Steifel (1952) or its analogs
Paige and Saunders (1982).
). One can
carry out the optimization iteratively with the help of the
conjugate-gradient method Hestenes and Steifel (1952) or its analogs
Paige and Saunders (1982).