




Next: Acknowledgments
Up: Data regularization as an
Previous: Model-space regularization
The data-space regularization approach is closely related to the
concept of model preconditioning Nichols (1994).
Regarding the operator 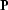 from equation (
from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as a
preconditioning operator, we can introduce a new model
) as a
preconditioning operator, we can introduce a new model 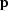 with
the equality
with
the equality
| 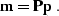 |
(21) |
The residual vector  for the data-fitting
equation (
for the data-fitting
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be defined by the relationship
) can be defined by the relationship
| 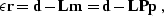 |
(22) |
where  is the scaling parameter from
equation (
is the scaling parameter from
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Let us consider a compound model
). Let us consider a compound model
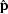 , composed of the preconditioned model vector
, composed of the preconditioned model vector
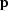 and the residual
and the residual  . With respect to the compound
model, we can rewrite equation (
. With respect to the compound
model, we can rewrite equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as
) as
| ![\begin{displaymath}
\left[\begin{array}
{cc} \bold{L P} & \epsilon \bold{I} \end...
...} \end{array}\right] =
\bold{G_d} \hat{\bold{p}} = \bold{d}\;,\end{displaymath}](img57.gif) |
(23) |
where 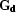 is a row operator:
is a row operator:
| ![\begin{displaymath}
\bold{G_d} = \left[\begin{array}
{cc} \bold{L P} &
\epsilon \bold{I} \end{array}\right]\;,\end{displaymath}](img59.gif) |
(24) |
and 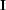 represents the data-space identity operator.
represents the data-space identity operator.
System (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is clearly underdetermined with respect to
the compound model
) is clearly underdetermined with respect to
the compound model 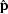 . If from all possible solutions of
this system we seek the one with the minimal power
. If from all possible solutions of
this system we seek the one with the minimal power 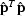 , the formal (ideal) result takes the well-known form
, the formal (ideal) result takes the well-known form
| ![\begin{displaymath}
<\!\!\hat{\bold{p}} = \left[\begin{array}
{c}
<\!\!\bold{p}...
... \epsilon^2 \bold{I}\right)^{-1} \bold{d}\end{array} \right]\;.\end{displaymath}](img61.gif) |
(25) |
Applying equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we obtain the corresponding
estimate
), we obtain the corresponding
estimate 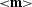 for the initial model
for the initial model 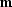 , which
is precisely equivalent to equation (
, which
is precisely equivalent to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). This proves the
legitimacy of the alternative data-space approach to data
regularization: the model estimation is reduced to least-square
minimization of the specially constructed compound model
). This proves the
legitimacy of the alternative data-space approach to data
regularization: the model estimation is reduced to least-square
minimization of the specially constructed compound model
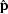 under the constraint (
under the constraint (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
Although the two approaches lead to similar theoretical results, they
behave quite differently in the process of iterative optimization. In
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I illustrate this fact with many examples
and show that in the case of incomplete optimization, the second
(preconditioning) approach is generally preferable.
, I illustrate this fact with many examples
and show that in the case of incomplete optimization, the second
(preconditioning) approach is generally preferable.
The next chapter addresses the choice of the forward interpolation
operator 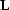 - the necessary ingredient of the iterative data
regularization algorithms.
- the necessary ingredient of the iterative data
regularization algorithms.





Next: Acknowledgments
Up: Data regularization as an
Previous: Model-space regularization
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as a
preconditioning operator, we can introduce a new model
) as a
preconditioning operator, we can introduce a new model ![]() from equation (
from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as a
preconditioning operator, we can introduce a new model
) as a
preconditioning operator, we can introduce a new model ![]() with
the equality
with
the equality
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be defined by the relationship
) can be defined by the relationship
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Let us consider a compound model
). Let us consider a compound model
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as
) as
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is clearly underdetermined with respect to
the compound model
) is clearly underdetermined with respect to
the compound model ![]() . If from all possible solutions of
this system we seek the one with the minimal power
. If from all possible solutions of
this system we seek the one with the minimal power ![]() , the formal (ideal) result takes the well-known form
, the formal (ideal) result takes the well-known form
![\begin{displaymath}
<\!\!\hat{\bold{p}} = \left[\begin{array}
{c}
<\!\!\bold{p}...
... \epsilon^2 \bold{I}\right)^{-1} \bold{d}\end{array} \right]\;.\end{displaymath}](img61.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we obtain the corresponding
estimate
), we obtain the corresponding
estimate ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). This proves the
legitimacy of the alternative data-space approach to data
regularization: the model estimation is reduced to least-square
minimization of the specially constructed compound model
). This proves the
legitimacy of the alternative data-space approach to data
regularization: the model estimation is reduced to least-square
minimization of the specially constructed compound model
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I illustrate this fact with many examples
and show that in the case of incomplete optimization, the second
(preconditioning) approach is generally preferable.
, I illustrate this fact with many examples
and show that in the case of incomplete optimization, the second
(preconditioning) approach is generally preferable.
![]() - the necessary ingredient of the iterative data
regularization algorithms.
- the necessary ingredient of the iterative data
regularization algorithms.