Next: ENERGY FLUX Up: Waves in layered media Previous: REFLECTION AND TRANSMISSION COEFFICIENTS

THE LAYER MATRIX

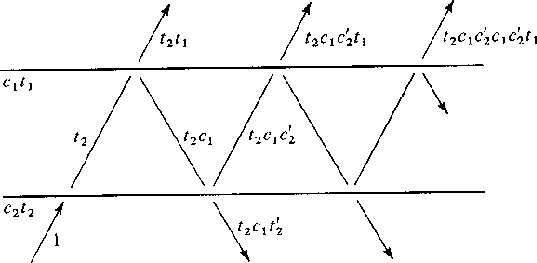Consider a layer with waves reverberating in it as shown in Figure 4.

8-4
Figure 4 Some rays corresponding to resonance in a layer.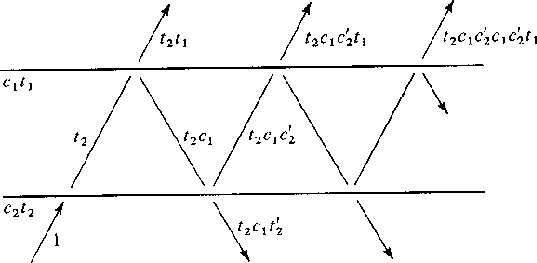

Let the delay operator Z refer to the time delay of a travel path across the layer and back again. The wave seen above the layer is an infinite sequence that is expressible as a simple denominator (because $1+X+X^2+X^3+\cdots = 1/(1-X)$ ).

$\begin{eqnarraystar} t_2 t_1 [1 + c_1 c^{'}_{2}Z + (c_1 c^{'}_{2})^2 Z^2 + \cdots ] \eq {t_2 t_1 \over 1 - c_1 c^{'}_{2}Z} \end{eqnarraystar}$

It is no accident that the infinite series may be summed. We will soon see that for n layers the waves, which are of infinite duration, may be expressed as simple polynomials of degree n. We consider many layers and the general problem of determining waves given reflection coefficients.

Equation (11) relates to Figure 5 and shows how from the waves U and D' we extrapolate into the future to get U' and D.

8-5
Figure 5 Waves incident and reflected from an interface.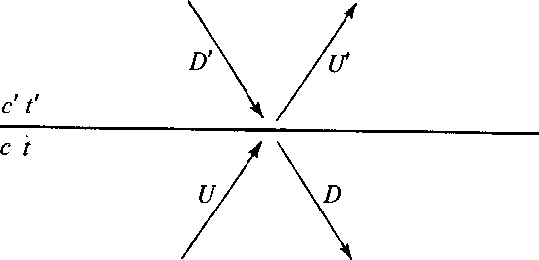

$\begin{eqnarray} U' & = & tU + c'D' \nonumber \\ D & = & cU + t'D'\end{eqnarray}$

(11)

Let us rearrange (11) to get U' and D' on the right and U and D on the left to get an equation which extrapolates from the primed medium to the unprimed medium. We get

$\begin{eqnarraystar} - tU \quad \quad & = & -U' + c'D' \\ - cU + D & = & \qquad \quad t'D'\end{eqnarraystar}$

Arrange to matrix form

$\begin{eqnarraystar} \left[ \begin{array} {ll} -t & 0 \\ -c & 1 \end{array} \r... ...ght] \; \left[ \begin{array} {c} U \\ D \end{array} \right]'\end{eqnarraystar}$

Premultiply by the inverse of the left-hand matrix

$\begin{eqnarraystar} \left[ \begin{array} {c} U \\ D \end{array} \right] & = ... ...ht] \; \left[ \begin{array} {c} U \\ D \end{array} \right]'\end{eqnarraystar}$

getting a result we want, an equation to extrapolate the infinitesimal distance from the bottom of one layer to the top of the next.

$\begin{displaymath} \left[ \begin{array} {c} U \\ D \end{array} \right] \eq {1... ...ight] \; \left[ \begin{array} {c} U \\ D \end{array} \right]'\end{displaymath}$ (12)

Now we consider a layered medium where each layer has the same travel-time thickness [Goupillaud medium]. Presumably, any continuously variable medium can be approximated this way. Examine the definitions in the layered medium in Figure 6.

8-6
Figure 6 Goupillaud-type layered medium (layers have equal travel time).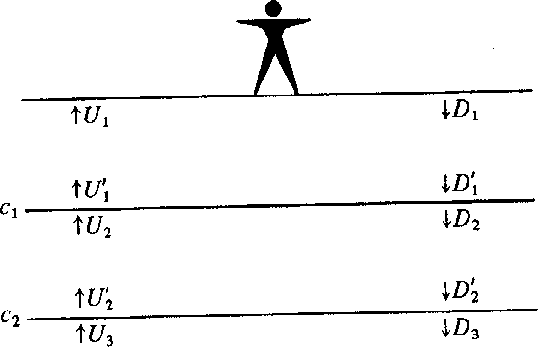

For this arrangement of layers, (12) may be written

$\begin{eqnarraystar} \left[ \begin{array} {c} U \\ D \end{array} \right]_{k+1}... ... \begin{array} {c} U \\ D \end{array} \right]'_{k} \nonumber\end{eqnarraystar}$

Let $Z = e^{i\omega T}$ where T, the two-way travel time, equals the data sampling interval. Clearly, multiplication by $\sqrt{Z}$ is equivalent to delaying a function by T/2, the travel time across a layer. This gives in the kth layer a relation between primed and unprimed waves.

$\begin{displaymath} \left[ \begin{array} {l} U \\ D \end{array} \right]'_k \eq... ...ght] \; \left[ \begin{array} {c} U \\ D \end{array} \right]_k\end{displaymath}$ (13)

Inserting (13) into (12) we get a layer matrix that takes us from the top of one layer to the top of the next deeper one.

$\begin{eqnarray} \left[ \begin{array} {c} U \\ D \end{array} \right]_{k+1} & ... ...ight] \; \left[ \begin{array} {c} U \\ D \end{array} \right]_k\end{eqnarray}$

(14)

Next: ENERGY FLUX Up: Waves in layered media Previous: REFLECTION AND TRANSMISSION COEFFICIENTS

Stanford Exploration Project
3/1/2001

	$\begin{eqnarray} U' & = & tU + c'D' \nonumber \\ D & = & cU + t'D'\end{eqnarray}$
		(11)

	$\begin{eqnarraystar} - tU \quad \quad & = & -U' + c'D' \\ - cU + D & = & \qquad \quad t'D'\end{eqnarraystar}$

	$\begin{eqnarraystar} \left[ \begin{array} {c} U \\ D \end{array} \right] & = ... ...ht] \; \left[ \begin{array} {c} U \\ D \end{array} \right]'\end{eqnarraystar}$

	$\begin{eqnarray} \left[ \begin{array} {c} U \\ D \end{array} \right]_{k+1} & ... ...ight] \; \left[ \begin{array} {c} U \\ D \end{array} \right]_k\end{eqnarray}$

		(14)