ENERGY FLUX

If there is energy flowing through a stack of layers, there should be the same energy flow through the kth layer as through the (k + 1)st layer. Otherwise, there would be an energy sink or source at the layer boundary. Let us guess that the net upward flow of energy (energy flux) at any frequency $\omega$ in the (k+1)st layer is given by  

$$\mbox{flux} (\omega) \eq Y_k \left[ U(Z) \bar{U} \left( {1 ... ...\right) - D(Z) \bar{D} \left( {1 \over Z} \right) \right]_{k+1}$$ (15)

Inserting equation (14) into equation (15) (and using a few simplifications all spelled out in FGDP) we deduce the principle that the energy flux across any layer matches that across the neighboring layer.  

$$Y_{k+1} \left[ U \left( {1\over Z} \right) U(Z) - D \left( ... ...r Z} \right) U(Z) - D \left( {1 \over Z} \right) D(Z) \right]_k$$ (16)

Since the flux is the same in any two adjacent layers, it must be the same in all the layers. This energy flux theorem leads quickly to some sweeping statements about the waveforms scattered from layered structures.

 

8-7 Figure 7 The reflection seismology geometry. The person sends an impulse down. The earth sends back -R(Z). Since the surface is perfectly reflective, it sends R(Z) back down. Escaping from the bottom is a wave E(Z) heading to infinity.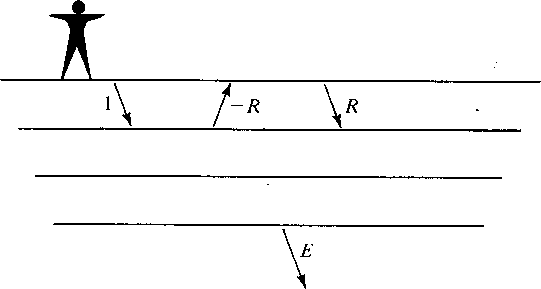

Figure 7 shows the basic geometry of reflection seismology. Applying the energy flux theorem to this geometry we may say that the energy flux in the top layer equals that in the lower halfspace so or  

$$1 + R \left( {1 \over Z} \right) + R(Z) \eq {Y_k \over Y_1}\ E \left( {1 \over Z} \right) E(Z)$$ (17)

This result is amazing. Nothing in life led me to suspect it before I found it. It says, if we were to observe the escaping wave E(Z), we could by autocorrelation construct the waveform seen at the surface. This result has no practical use, but a slightly different arrangement does.

The escaping wave E(Z) turns out to be the same as the earthquake wave X(Z) in Figure 8.

 

E8-3-5 Figure 8 Earthquake seismology geometry. An impulse 1 is incident from below. The waveform X(Z) is incident upon the free surface and is reflected back down. The waveform P(Z) scatters back into earth.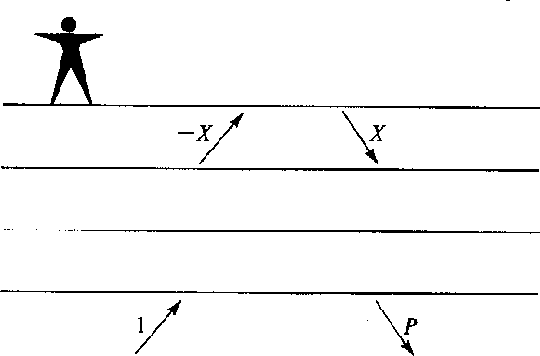

This can be shown algebraically (see exercises) or deduced as a consequence of the reciprocity principle (the idea that interchanging source and receiver location yields the same response). Notice that the incident earthquake ``1'' need not be an impulsive wave; it only need have the autocorrelation of an impulsive wave. This conclusion leads to the remarkable hypothesis that the autocorrelation of natural noises (microseism) gives reflection seismograms. This concept has proven useful in solar seismology, but a variety of practical factors (principally spatial distribution of stations) has limited its utility on the earth so far.

A more obvious result applies to the earthquake seismology geometry in Figure 8. Applying the energy flux theorem to this geometry we obtain

$$Y_1 \left[ X \left( {1\over Z} \right) X(Z) - X \left( {1\ov... ...ht] \eq Y_k \left[ 1 - P(Z)P \left( {1 \over Z} \right) \right]$$

or  

$$1 \eq P(Z)P \left( {1 \over Z} \right)$$ (18)

The interpretation of the result is that the backscattered waveform P(Z) has the form of an all-pass filter. (An all-pass filter has a constant energy spectrum and an arbitrary phase spectrum.) This result may have been anticipated on physical grounds since all the energy which is incident is ultimately reflected without attenuation; thus the only thing which can happen is that there will be frequency-dependent delay.