




Next: INSTABILITY
Up: DAMPED OSCILLATION
Previous: Spectrum of a pole
A general model for filtering includes both convolution
(numerator Z-transforms) and feedback filtering
(denominator Z-transforms):
| 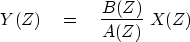 |
(40) |
There are a variety of ways
to implement equation (40) in a computer.
We could do the polynomial division X(Z)/A(Z) first
and then multiply (convolve) with B(Z),
or we could do the multiplication first and the division later.
Alternately, we could do them simultaneously
if we identified coefficients of A(Z)Y(Z)=B(Z)X(Z)
and solved for recursive equations, as we did for (34).
The rational filter is more powerful than either a purely numerator
filter or a purely denominator filter because,
like its numerator part, the rational filter
can easily destroy any frequency totally,
and, like its denominator part,
it can easily enhance any frequency without limit.
Finite-difference solutions of differential equations
often appear as rational filters.
EXERCISES:
- Consider equation (40).
What time-domain recurrence (analogous to equation (34)) is implied?





Next: INSTABILITY
Up: DAMPED OSCILLATION
Previous: Spectrum of a pole
Stanford Exploration Project
10/21/1998