INSTABILITY

Consider the example B(Z) = 1 - Z/2. The inverse  

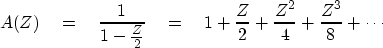$$A(Z) \eq {1 \over 1 - {Z \over 2}} \eq 1 + {Z \over 2} + {Z^2 \over 4} + {Z^3 \over 8} + \cdots$$ (41)

can be found by a variety of familiar techniques, such as (1) polynomial division, (2) Taylor's power-series formula, or (3) the binomial theorem. In equation (41) we see that there are an infinite number of filter coefficients, but because they drop off rapidly, approximation in a computer presents no difficulty.

We are not so lucky with the filter B(Z) = 1 - 2Z. Here we have  

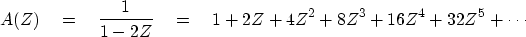$$A(Z) \eq {1 \over 1-2Z} \eq 1 + 2Z + 4Z^2 + 8Z^3 + 16Z^4 + 32Z^5 + \cdots$$ (42)

The coefficients of this series increase without bound. This is called ``instability.'' The outputs of the filter A(Z) depend infinitely on inputs of the infinitely distant past. (Recall that the present output of A(Z) is a₀ times the present input x₁, plus a₁ times the previous input x_t-1, etc., so a_n represents memory of n time units earlier.) This example shows that some filters B(Z) will not have useful inverses A(Z) determined by polynomial division. 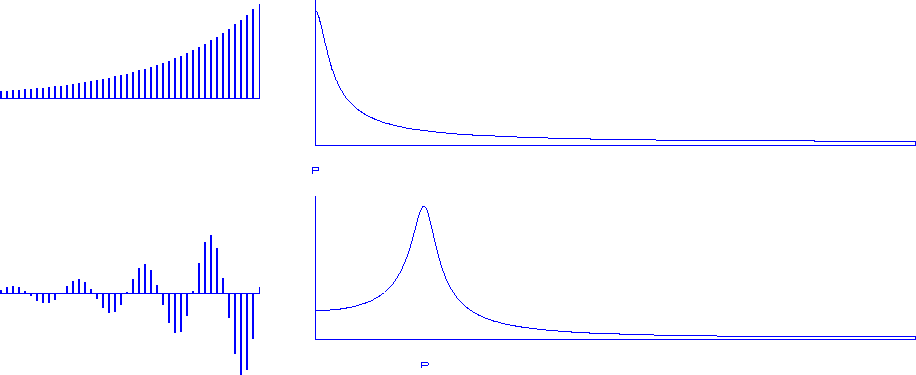Two sample plots of divergence are given in Figure 11.

 

diverge
Figure 11 Top: the growing time function of a pole inside the unit circle at zero frequency. Bottom: at a nonzero frequency. Where the time axis is truncated, the signals are growing, and they will increase indefinitely.

For the filter 1-Z/Z₀ with a single zero, the inverse filter has a single pole at the same location. We have seen a stable inverse filter when the pole |Z_p|>1 exceeds unity and instability when the pole |Z_p|<1 is less than unity. Occasionally we see complex-valued signals.

Stability for wavelets with complex coefficients is as follows: if the solution value Z₀ of B(Z₀) = 0 lies inside the unit circle in the complex plane, then 1/B(Z) will have coefficients that blow up; and if the root lies outside the unit circle, then the inverse 1/B(Z) will be bounded.