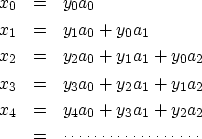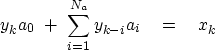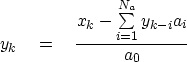# polynomial division feedback filter: Y(Z) = X(Z) / A(Z)
#
subroutine polydiv( na, aa, nx, xx, ny, yy )
integer na # number of coefficients of denominator
integer nx # length of the input function
integer ny # length of the output function
real aa(na) # denominator recursive filter
real xx(nx) # input trace
real yy(ny) # output trace, as long as input trace.
integer ia, iy
do iy= 1, ny
if( iy <= nx)
yy(iy) = xx(iy)
else
yy(iy) = 0.
do iy= 1, na-1 { # lead-in terms
do ia= 2, iy
yy(iy) = yy(iy) - aa(ia) * yy(iy-ia+1)
yy(iy) = yy(iy) / aa(1)
}
do iy= na, ny { # steady state
do ia= 2, na
yy(iy) = yy(iy) - aa(ia) * yy(iy-ia+1)
yy(iy) = yy(iy) / aa(1)
}
return; end