




Next: Causes of seismic image
Up: Detection of seismic discontinuities
Previous: Future
In this chapter
I explore three discontinuity attributes:
standard edge enhancement,
plane-wave misfit, and
prediction error.
I illustrate each approach on one
synthetic (Figure 4)
and
two seismic images
(Figures
7 and 11).
The first seismic image depicts a Gulf salt dome.
The faults of the image are sharp and well defined.
Bahorich et al illustrates the original coherency attribute
at the same image.
The second seismic image shows a North Sea horst and is the more
challenging test case.
The faults are smooth and difficult to find in the seismic time slice.
Bednar used the same image in the publication that describes his
discontinuity attribute.
Table 1:
Discontinuity attributes.
The table lists the various discontinuity attributes
that I explore in this thesis.
An attribute's label
identifies
the corresponding names of Figures.
The norm
 is the standard vector norm.
The vector
is the standard vector norm.
The vector 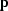 is an estimate of the local plane-wave normal.
The operator A represents a 3-D prediction-error operator.
The operators Ai are two-dimensional versions.
is an estimate of the local plane-wave normal.
The operator A represents a 3-D prediction-error operator.
The operators Ai are two-dimensional versions.
| Label |
Name |
Computation |
Output format |
| 4l |
|
|
|
| 4lGradient methods |
|
|
|
| Grad |
Gradient magnitude |
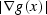 |
scalar at each pixel |
| Lap |
Laplace |
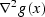 |
scalar at each pixel |
| 4l |
|
|
|
| 4lDip misfit methods |
|
|
|
| DXG |
Cross-product |
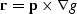 |
3 component vector |
| |
|
|
at each pixel |
| DXGLN |
Magnitude of r |
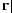 |
scalar at each pixel |
| DXGAA |
Backprojection of r |
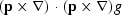 |
scalar at each pixel |
| 4l |
|
|
|
| 4lWaveform misfit methods |
|
|
|
| PPC |
Correlation of estimate |
![$Cor_z[g({\bf x}), f({\bf p} \cdot {\bf x})]$](img8.gif) |
scalar for each trace |
| |
and original |
|
of patch |
| 4l |
|
|
|
| 4lPrediction-error methods |
|
|
|
| Pef3d |
3-D PEF |
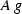 |
scalar at each pixel |
| XPef |
3 2-D PEF |
![${\bf \epsilon} = [A_x,A_y,A_z] g$](img10.gif) |
3 component vector |
| |
|
|
at each pixel |
| XPefLN |
Magnitude of  |
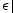 |
scalar at each pixel |
| XPefAA |
Backprojection of  |
![$[A_x,A_y,A_z] \cdot \epsilon$](img13.gif) |
scalar at each pixel |
The Table 1 lists the various methods that I include
in this publication.
The
standard edge enhancement techniques fail to differentiate
sedimentary beds and boundaries of sedimentary packages
(Figure 16).
However,
two-dimensional edge enhancement within a time slice
takes advantage of the dominant horizontal dip of sedimentary strata
and yields reasonable fault maps
(Figure 23).
Of all my discontinuity attributes,
the trace correlation of an image region and its
locally best-fitting plane wave
consistently yields
the clearest fault maps
(Figures 33 and 34).
Other measures of plane-wave misfit that I tested
generated only inferior fault images
(e.g., Figure 27).
The algorithm of my plane-wave correlation is,
similar to the computation of the commercial coherency attribute
by Bahorich and Farmer 1995.
Both processes certainly generate a similar discontinuity map of
the Gulf salt dome.
My plane-wave estimation is related to
Symes' differential semblance.
I derived the plane-wave estimation
by generalizing a dip estimation scheme by
Claerbout 1994.
Bednar derives his discontinuity attribute
from Claerbout's dip estimation, too.
Prediction-error is an unreliable and noisy discontinuity attribute.
The discontinuity map of the salt dome
(Figure 44)
shows the radiating faults,
and even resolves features within the salt. Unfortunately,
the image is obscured by noise.
Even worse,
the prediction error filter predicts and removes almost
all features of the smoother North Sea horst image
(Figure 45).
Prediction-error images tend to be white Jain (1989), since
the filter removes the predictable correlated
components of its input.
Claerbout 1992
introduced a combination of two two-dimensional filters
that detect and suppress a three-dimensional plane-wave.
I added a third prediction-error filter, which
generalizes Claerbout's intuitive, original formulation.
The three prediction-errors are linked to the cross-product
expression of my plane-wave formulation.
The prediction-error filters' removal
of all image features
in the North Sea case
suggests limiting the predictive power of the filters.
In earlier studies Schwab et al. (1996); Schwab (1997),
I limited the number of iterations, and
I enlarged and pre-whitened the training patches.
However, the prediction-error maps were still white.
The data dependent attribute measures -
misfit of local plane wave and the prediction error -
depend on local estimation within stationary local image patches.
Since patches that contain a discontinuity are nonstationary,
the attributes usually yield a large output anywhere
within such a patch.
(Figures 26
or 36. Note, that the image is composed
of about 300 patches.
A side of the cubic patch is 12 pixels long;
about one seventh of the total data cube edge of 80 pixels.)
The schemes detect if a patch contains a discontinuity,
but do not pinpoint the discontinuity within the patch.
Consequently, the data dependent schemes are limited
to a resolution the size of their patches.





Next: Causes of seismic image
Up: Detection of seismic discontinuities
Previous: Future
Stanford Exploration Project
3/8/1999