Prediction error

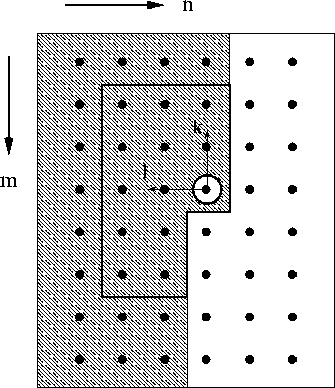Prediction error is a discontinuity attribute that removes the predictable image components and reveals the unpredictable. To use prediction error as a discontinuity attribute - the original goal and starting point of my project - one has to devise a prediction-error computation that predicts and removes the plane-wave volumes of sedimentary layers but that is incapable of predicting the discontinuities.

Prediction-error filters Claerbout (1992); Jain (1989) remove the image component that is predictable as a linear combination of its neighboring values. Given a two-dimensional image u(m,n) and the linear prediction estimate

the prediction error is simply .

The region S_x defines which neighboring values contribute to the linear prediction. Causal predictions, that involve regions of the shape shown in Figure 35, lead to white noise driven output images. The region is called causal since given a hypothetical scan from top to bottom and left to right all points of S_x lie to one-side of the predicted value u(m,n).

 

pefDomain Figure 35 Prediction-error domain. The causal domain ensures that the output of the prediction-error filter tends to be white noise.

To compute the prediction error of a given stationary image, we first find the prediction coefficients a(k,l) that minimize the prediction error for all pixels of the input image. Once the prediction coefficients are known, the convolution

computes the prediction error. In particular, a prediction-error filter potentially zeroes a random plane-wave, or a superposition of random plane waves, or a superposition of random constant-amplitude lines. I represent the prediction-error computation as

where g is the input image, A is the prediction-error operator, and $\epsilon$ the residual prediction error.

To compute the prediction error of a nonstationary image, I, as usual, divide the image into stationary patches, compute the prediction error for each patch, and merge the patches containing the local prediction error into a single quilt. All result images of this section are smoothed along the vertical axis to suppress the prediction error's tendency to enhance high-frequency noise of the original unfiltered image.