Accuracy tests

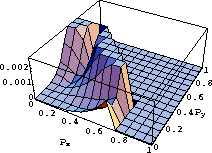Before we use the new dispersion relation to derive an acoustic wave equation we must first investigate how accurate is this dispersion equation in representing elastic media. Specifically, I will measure the error associated with equation 17 with respect to the elastic equation. The dispersion relation for elastic media is evaluated numerically. Since the isotropic dispersion relation is independent of the shear wave velocity, and it's acoustic version is exact, the errors corresponding to the acoustic dispersion equation is expected to be dependent on the strength of anisotropy.

 

error1 Figure 1 Errors in pz evaluated using equation 17 measured in s/km as a function of px and py. The orthorhombic model has vv=1 km/s, v1=1.1 km/s, $\eta_1=0.1$, v2=1.2 km/s, $\eta_2=0.2$, and $\delta$=0.1. The shear wave velocities for the elastic medium equal 0.5 km/s.

Figure 1 shows a 3-D surface plot of the error in p_z evaluated using equation 17 as a function p_x and p_y. The error is given by the difference between p_z measured using equation 17 and that using the elastic equation, with non-zero shear wave velocities. In fact, the reference elastic medium has shear wave velocities equal to half the vertical P-wave velocity ( v_s1= v_s2= v_s3=0.5 km/s). Since the vertical P-wave velocity in all the examples equal 1 km/s, p_z can have a maximum value of 1 and a minimum of zero. The Orthorhombic model used in Figure 1 has v₁=1.1 km/s, $\eta_1=0.1$, v₂=1.2 km/s, $\eta_2=0.2$, and $\delta$=0.1. This model is practical with a strength of anisotropy that is considered moderate. Clearly, the errors given by a maximum value of 0.002 is extremely small suggesting that equation 17 is accurate for this case. Equation 17 is exact for zero and 90 degree dip reflectors, and therefore, most of the errors occur at angles in between. However, such errors are clearly small.

 

error1s Figure 2 Errors in pz evaluated using equation 17 measured in s/km as a function of px and py. The orthorhombic model has vv=1 km/s, v1=1.1 km/s, 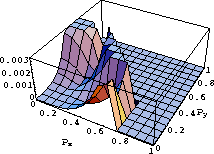$\eta_1=0.1$, v2=1.2 km/s, $\eta_2=0.2$, and $\delta$=0.1. Here, the elastic medium has vs1=0.6 km/s, vs2=0.7 km/s,and vs3=0.7 km/s.

From my earlier experience Alkhalifah (1997a), errors in the acoustic approximations increase with increasing shear wave velocity. Obviously, if shear wave velocity equals zero no errors are incurred. Figure 2 shows the same model used in Figure 1, but with higher shear wave velocities. Specifically, v_s1=0.6 km/s, v_s2=0.7 km/s,and v_s3=0.7 km/s. Here, the vertical S-wave to P-wave velocity ratio equal 0.6, which can be considered as an upper limit for most practical models in the subsurface. Yet, the errors given by the acoustic approximations (maximum error equal to 0.003) is still extremely small.

 

error2 Figure 3 Errors in pz evaluated using equation 17 measured in s/km as a function of px and py. The orthorhombic model has vv=1 km/s, v1=0.9 km/s, 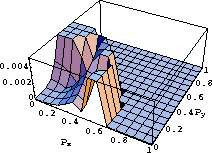$\eta_1=0.6$, v2=1.2 km/s, $\eta_2=0.4$, and $\delta$=0.3. Here, the elastic medium has vs1=0.7 km/s, vs2=0.8 km/s, and vs3=0.8 km/s.

To test the limits of the new dispersion relation, I use an orthorhombic model of strong anisotropy. Specifically, v₁=0.9 km/s, $\eta_1=0.6$, v₂=1.2 km/s, $\eta_2=0.4$, and $\delta$=0.3. The strength of anisotropy in this test is given by the high $\eta_1$, $\eta_2$, and $\delta$ values. I also use for the elastic equation high shear wave velocities given by v_s1=0.7 km/s, v_s2=0.8 km/s,and v_s3=0.8 km/s. Figure 3 shows a 3-D surface plot of the error in p_z evaluated using equation 17 as a function p_x and p_y. The errors are slightly larger than those in Figures 1 and 2, but overall acceptable. The maximum error of about 0.004 is much smaller than the possible range of p_z.

 

error2s Figure 4 Errors in pz evaluated using equation 17 measured in s/km as a function of px and py. The orthorhombic model has vv=1 km/s, v1=0.9 km/s, 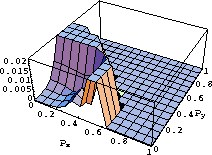$\eta_1=0.6$, v2=1.2 km/s, $\eta_2=0.4$, and $\delta$=0.3. Here, the elastic medium has vs1=0.9 km/s, vs2=0.9 km/s, and vs3=0.9 km/s.

However, there is a limit to what kind of shear wave velocities the elastic media can have before this acoustic approximation breaks down. Figure 4 shows the errors for the same model in Figure 3 with even higher shear wave velocities. Specifically, v_s1=v_s2=v_s3=0.9 km/s. Suddenly the acoustic approximation incurs large errors, up to 0.02 in the value of p_z over a possible range of 1. However, note that such a model given by v_s1=v_s2=v_s3=0.9 km/s is highly unlikely considering that the vertical P-wave velocity equal 1 km/s. This constitutes an extreme orthorhombic anisotropy model that probably does not exist in the subsurface.

 

errorVTI Figure 5 Errors in pz evaluated using equation 17 measured in s/km as a function of px and py. The VTI model has vv=1 km/s, v1=1.1 km/s, $\eta_1=0.1$, v2=1.1 km/s, $\eta_2=0.1$, and $\delta$=0.

For comparison, Figure 5 shows this same error test, however for a VTI model. The model is given by v₁=1.1 km/s, $\eta_1=0.1$, v₂=1.1 km/s, $\eta_2=0.1$, and $\delta$=0. The error size is very similar to that in Figure 1, but more symmetric since the VTI model exerts symmetry on the horizontal plane.

In summary, the dispersion relation given by equation 17 is, for all practical purposes, exact. Thus, the acoustic wave equation extracted from this dispersion relation is expected to be accurate as well.