The dispersion relation

Seismic reflection data are often recorded on the Earth surface. Therefore, an equation that describes the vertical slowness as a function of the horizontal one, the dispersion relation, is a key equation for imaging such data. In fact, reflection seismic data explicitly provides horizontal slowness information given by the slope of the reflections.

However, a simple P-wave analytical equation that describes the vertical slowness as a function of the horizontal one does not exist in a practical form for orthorhombic media. Because obtaining such an equation requires solving for the roots of a cubic polynomial as a function of the squared vertical slowness. On the other hand, setting all three shear wave velocities to zero will reduce the cubic equation to a linear one. The influence of the shear-wave velocities on P-wave propagation is small. This is a general statement that holds for most anisotropies, but have been proven extensively for transversely isotropic media. The setting of the shear velocity to zero, as we will see later, will not compromise the accuracy of the equations for kinematic or dynamic uses.

To obtain the dispersion relation for orthorhombic anisotropy we must first derive the Christoffel equation for such media. A general form for the Christoffel equation in 3-D anisotropic media is given by

$$\Gamma_{ik}(x_s,p_i)= a_{ijkl}(x_s) p_j p_l,$$

with

$$p_i=\frac{\partial \tau}{\partial x_i},$$

$$a_{ijkl}=c_{ijkl} / \rho,$$

where p_i are the components of the phase vector, $\tau$ is the traveltime along the ray, $\rho$ is the bulk density, x_s are the Cartesian coordinates for position along the ray, s=1,2,3.

For orthorhombic media, the Christoffel equation slightly simplifies, and in its matrix form (using A_ij instead of a_ijkl) is given by  

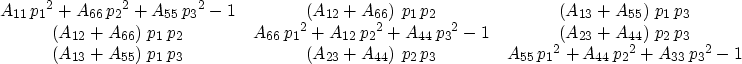$$\matrix{ {A_{11}}\,{{{p_1}}^2} + {A_{66}}\,{{{p_2}}^2} + {... ...}^2} + {A_{44}}\,{{{p_2}}^2} + {A_{33}}\,{{{p_3}}^2} -1 \cr }$$ (14)

where A_ij are the density normalized elastic coefficients ($A_{ij}=\frac{C_{ij}}{\rho}$).

Setting all shear wave velocities (v_s1, v_s2, and v_s3) to zero and using Tsvankin's 1997 parameter representation, the Christoffel equation reduces to  

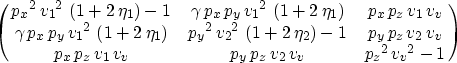$$\left(\matrix{ {{{p_x}}^2}\,{{{v_1}}^2}\, \left( 1 + 2\,{{\... ...{p_z}\,{v_2}\,{v_v} & {{{p_z}}^2}\,{{{v_v}}^2}-1 \cr }\right)$$ (15)

Here we have replaced p₁ with p_x, p₂ with p_y, and p₃ with p_z, for convenience. Taking the determinant of (15) gives a linear equation in p_z², as follows

$$\begin{eqnarray} {\bf Det} =-1 + {{{p_z}}^2}\,{{{v_v}}^2} + {{{p_y}}^2}\,{{{v_... ...}^2}\,{{{v_2}}^2}\,{{{v_v}}^2}\,{{\eta }_1}\, {{\eta }_2} \right)\end{eqnarray}$$ (16)

Setting equation (16) to zero and solving for p_z provides the dispersion relation for orthorhombic media as follow

p_z²=

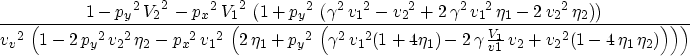$$\begin{eqnarray} {\frac{1 - {{{p_y}}^2}\,{{{V_2}}^2}\, - {{{p_x}}^2}\,{{{V_1}}^... ...} (1 - 4\,{{\eta }_1}\,{{\eta }_2}) \right) \right) \right) }}\end{eqnarray}$$ (17)

Each principal plane of the orthorhombic model is VTI in nature, thus setting p_y=0 in equation (17) gives

$$p_z^2= \frac{1}{v_v^2} \left( 1-\frac{v_1^2 p_x^2}{1-2 \eta_1 v_1^2 p_x^2} \right),$$

which is simply the dispersion relation for the VTI case, shown by Alkhalifah (1997a).

Note that the vertical velocity appears only once in equation (17) and thus the vertical-time based dispersion relation, like in the case of VTI media, become vertical velocity independent. This feature is shown approximately by Grechka and Tsvankin (1997) using numerical methods, and is shown exactly here.