




Next: The dispersion relation
Up: Alkhalifah: Wave equation for
Previous: Introduction
Unlike in VTI media, where the model is fully characterized by 5 parameters, in orthorhombic
media we need 9 parameters for full characterization. However, like in VTI media, not
all parameters are expected to influence P-wave propagation to a detectable degree. Therefore, alternative parameter
representation is important to simplify the problem to a level where key parameter dependencies are recognizable.
The stiffness tensor cijkl for orthorhombic media can be represented in a
compressed two-index notation (the so-called ``Voigt recipe'') as follows:
|  |
(1) |
In VTI media, c11=c22, c13=c23, c44=c55, c12=c11-2 c44,
and thus the number of independent parameters reduce
from 9 to 5. With additional constraints given by the isotropic model the number of independent parameters will
ultimately reduce to two.
Significant progress, however, can be made by combining the stiffnesses in such a way that will simplify
analytic description of seismic velocities.
Tsvankin (1997) suggested a parameterization similar to what Thomsen (1986) used for
VTI media and to what Alkhalifah and Tsvankin (1995) added for processing purposes, namely the 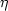 parameter.
I will list the nine parameters needed to characterize orthorhombic media below. However, for convenience in later
derivations, I will replace the
parameter.
I will list the nine parameters needed to characterize orthorhombic media below. However, for convenience in later
derivations, I will replace the  parameters with
parameters with 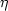 parameters and use slightly
different notations than those given by Tsvankin (1997).
In summary,
these nine parameters are related to the elastic coefficients as follows:
parameters and use slightly
different notations than those given by Tsvankin (1997).
In summary,
these nine parameters are related to the elastic coefficients as follows:
- the P-wave vertical velocity:
| 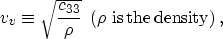 |
(2) |
- the vertical velocity of the S-wave polarized in the
x1-direction:
| 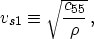 |
(3) |
- the vertical velocity of the S-wave polarized in the
x2-direction:
| 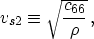 |
(4) |
- the horizontal velocity of the S-wave polarized in the
x3-direction:
| 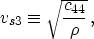 |
(5) |
- the NMO P-wave velocity for horizontal reflectors in the
[x1,x3] plane:
| 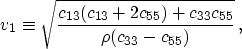 |
(6) |
- the NMO P-wave velocity for horizontal reflectors in the
[x2,x3] plane:
| 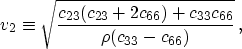 |
(7) |
- the
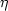 parameter in the [x1,x3] symmetry
plane:
parameter in the [x1,x3] symmetry
plane:
| 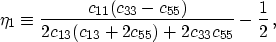 |
(8) |
- the
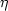 parameter in the [x2,x3] symmetry
plane:
parameter in the [x2,x3] symmetry
plane:
| 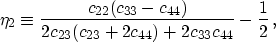 |
(9) |
- the
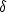 parameter in the [x1,x2]
plane (x1 plays the role of the symmetry axis):
parameter in the [x1,x2]
plane (x1 plays the role of the symmetry axis):
| 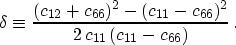 |
(10) |
This notation preserves the attractive features of Thomsen parameters in describing velocities,
and traveltimes. They also provide a simple way to measure anisotropy, since the dimensionless
parameters in the new representation equal zero when the medium is isotropic. The notation used above, also,
simplify description of time-related processing equations.
To ease some of the derivations later in this paper I will also use the horizontal velocity in the x1 direction:
| 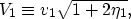 |
(11) |
and the horizontal velocity in the x2 direction:
| 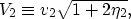 |
(12) |
Both horizontal velocities are given in terms of the above parameters and thus do not add to the number of
independent parameters required to represent orthorhombic media. Finally, I will use 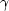 as follows
as follows
| 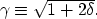 |
(13) |
Thus, for isotropic media 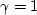 .
.





Next: The dispersion relation
Up: Alkhalifah: Wave equation for
Previous: Introduction
Stanford Exploration Project
8/21/1998


![]() parameter.
I will list the nine parameters needed to characterize orthorhombic media below. However, for convenience in later
derivations, I will replace the
parameter.
I will list the nine parameters needed to characterize orthorhombic media below. However, for convenience in later
derivations, I will replace the ![]() parameters with
parameters with ![]() parameters and use slightly
different notations than those given by Tsvankin (1997).
In summary,
these nine parameters are related to the elastic coefficients as follows:
parameters and use slightly
different notations than those given by Tsvankin (1997).
In summary,
these nine parameters are related to the elastic coefficients as follows: